Source:
From all the zillions of pages on the web I have tried to gather the best feeds available for you, enjoy it! DISCLAIMER - BE CAREFUL READING THEM - WE ARE NOT RESPONSABLE OF WHAT THE AUTHORS SAY.
Sunday 30 January 2022
Leaked Database Shows U.S. Military Disease Skyrocketing After Covid-19 Inoculations
Vaccinated Blood – The Dilemma Of COVID’s Experimental Transfusions
Source:
’Sullivan
Should we have the right to refuse a blood transfusion from the vaccinated for COVID-19? What about organs donated by the vaccinated?
In most nations anyone vaccinated for COVID-19 can donate blood immediately or shortly after being vaccinated despite the fact that the experimental product may induce life-threatening disorders in the recipients.
Donated blood will mix with yours and the worrisome injected spike proteins from the donor blood will circulate and merge into your body.
The vast majority of people, especially the media, are not addressing this issue. Concerned citizens should be writing to all health authorities, politicians and public health bodies and demand screening and separate blood banks and clear identification of vaccinated and unvaccinated blood. No one knows the long term safety data. This is a global experiment on humanity and it must be stopped!
Watch the video below to discern the level of threat.
Does anyone remember the fallout from the AIDS pandemic when infected donated blood destroyed the lives of thousands?
In the late 1970s and early 1980s, sufferers of the blood-clotting disorder haemophilia in the UK were given blood donated – or sold – by people who were infected with the HIV virus and hepatitis C.
According to The Guardian newspaper (July 11, 2017) haemophiliacs pressed for compensation after:
“4,800 of them were infected with hepatitis C, a virus that causes liver damage and can be fatal. Of those, 1,200 were also infected with HIV, which can cause Aids. Half – 2,400 – have now died.”
In 1991, when campaigners were threatening to take the government to court, it made ex-gratia payments to those infected with HIV, averaging £60,000 each, on condition that they dropped further legal claims. The extent of infection with hepatitis C was not discovered until years later.
Today, with the COVID19 experimental vaccines being blamed for over one million adverse reactions, we can be sure this story is another ticking time bomb in government failure.
[…]
Via https://alethonews.com/2021/06/08/vaccinated-blood-the-dilemma-of-covids-experimental-transfusions/
Saturday 29 January 2022
The true under reporting factor (URF) for miscarriages is 49.
Source:
https://jessicar.substack.com/p/the-true-under-reporting-factor-urf
Calculating the URF for miscarriages using the DMED as a base data set.
This article is about calculating the URF using the Defense Medical Epidemiology Database (DMED). It was released recently and contains breath-taking data. This data set is special because it contains up-to-date data for every individual in the U.S. military with regards to their existing diseases, medical history and personal data.
It is a highly controlled and closed data set: only Department of Defense (DOD) personnel are in this system and only medical providers can input data into this system. For anyone trash-talking VAERS due to its limitations, this is the data set for you. The U.S. military don’t screw around.
According to the data, the total number of spontaneous abortions (miscarriages) for the past 5 years (2016-2020) was 1,499. That’s about 300 spontaneous abortions per year for the past 5 years. According to VAERS data, in 2021 the number of reports of spontaneous abortions was 3,527.
Let’s calculate the background rate of spontaneous abortions using the DMED data. The total number of women enlisted and on active duty in the U.S. military in 2020 was 226,417 (this represents the 17.2% female population enrolled + active in 2020 (N = 1,333,822)). Therefore, the background rate based on DMED data is 132 spontaneous abortions per 100,000 women.
The number of females injected in the U.S. with at least one dose of COVID-19 product is 128,964,332 according to the CDC.1 Considering the 3,527 reports of spontaneous abortions to VAERS in 2021, the rate of reporting of spontaneous abortions in VAERS is 2.7/100,000 women. (Not all women in this group will be of child-bearing age.)
To get to the background rate in the DMED, we need to multiply our VAERS rate by 49. This means, the URF for spontaneous abortion in VAERS is 49. When we apply this URF we get 172,823 spontaneous abortions.
This is not refutable. The DMED data set is not up for interpretation even if you think that VAERS is. The background rate for spontaneous abortions is 132 per 100,000 women (or ~1/1000).
So there you have it. The URF for spontaneous abortions in VAERS is 49 based on the DMED data.
If you are looking for a great write-up on this story, go here.
It’s been pointed out by my colleague that the URF is likely even higher than this due to the fact that women on active duty are probably going to less likely to get pregnant than the general population. It’s a good point. Anyone want to take a crack at how to calculate that one?
UPDATE: MD has made a good point in the comments as well. The denominator should actually be the number of women injected of child-bearing age. According to the same CDC source as above, the number of injected people between the ages 12 and 39 is 92,317,670 and since females make up exactly half of this population, the denominator becomes 46,158,835. Thus, with this denominator, we have 7.6 spontaneous abortions per 100,000 women injected aged 12-39. The best I can do with the more appropriate denominator for the DMED data is individuals up to and including the age of 40. That’s not bad. This new denominator then becomes 98,240. Thus, the rate of spontaneous abortions in women of ‘child-bearing age’ in the military becomes report 305 per 100,000. Thus, the new URF would be 40.2
That would make the spontaneous abortion count associated with the COVID-19 injections 141,544.
I am sure this can be rendered even more precise but I am confident that the true number of women of child-bearing age who have suffered a spontaneous abortion in association with the COVID-19 injectable products is around 150,000.
In any case, it’s a bad situation. Thank you for the input everyone.
1- https://covid.cdc.gov/covid-data-tracker/#vaccination-demographic
2 - If we include women from the injected list who are 40-49 as well (because those eggies are still good in some of the oldies but mostly, I would say it’s the women at 40 or in the early 40s who would be considered child-bearing age), we get an URF of 55 yielding 193,324 women who’d suffered a spontaneous abortion.
Jessica Rose
Friday 28 January 2022
Sweden decides against vax for kids ages 5 to 12
Source:
https://stevekirsch.substack.com/p/sweden-decides-against-vax-for-kids
CNN didn't think this was newsworthy enough to mention, so I wanted to make sure everyone knew. Meanwhile, US Surgeon General says big tech should silence scientists like Malone who disagree with him.
Sweden couldn’t find any benefit of the COVID vaccines since the rates of serious disease are so low.
Here in the US, we can’t find any benefit either, but that doesn’t matter. In fact, the risk-benefit analysis is strongly negative. Here’s the risk benefit analysis for kids in the US done by Dr. Toby Rogers:
Nobody wants to discuss this analysis.
According to this article, U.S. Surgeon General Vivek Murthy in fact thinks that nobody should even know about analyses like this.
They are smart. They know that censorship is the only option when you don’t have any of the facts on your side.
Thursday 27 January 2022
Vaccinated account for 4 in every 5 Covid-19 Hospitalisations & Deaths in the past month
Source:
https://dailyexpose.uk/2022/01/27/4-in-5-covid-deaths-vaccinated-majority-triple-jabbed/
The latest Covid-19 Statistical report published by Public Health Scotland shows that the triple vaccinated have accounted for the vast majority of Covid-19 hospitalisations and deaths over the past month, witht the vaccinated population as a whole accounting for 4 in every 5 hospitalisations and deaths.
Public Health Scotland’s (PHS) weekly Covid-19 Statistical Report contains figures on Covid-19 cases, hospitalisations, and deaths by vaccination status and the latest report does not do anything to justify that the Covid-19 vaccines have a positive effect.
The following graph shows the number of Covid-19 hospitalisations by vaccination status in Scotland. The data has been extracted from table 14, found on page 44 of the PHS Covid-19 Statistical report published Wednesday 26th Jan 22.
Between 25th Dec 21 and 21st Jan 22 there were 3,096 Covid-19 hospitalisations recorded in Scotland, and the vaccinated population accounted for 81% of them, with the triple vaccinated accounting for 61% of all hospitalisations among the vaccinated, and the double jabbed accounting for 32%.
Each week since 25th Dec has seen the triple vaccinated population account for the most Covid-19 hospitalisations, with the double vaccinated not far behind, as can be seen in the following graph.
Hospitalisations among all demographics peaked in the week beginning 1st January except for the triple vaccinated who continued to record a large increase in hospitalisations in the week beginning 8th Jan 22, suggesting the third jab may have actually had a negative effect on recipients.
The following graph shows the number of Covid-19 deaths by vaccination status in Scotland. The data has been extracted from table 15, found on page 50 of the PHS Covid-19 Statistical report published Wednesday 26th Jan 22.
Between 18th Dec 21 and 14th Jan 22 there were 277 Covid-19 deaths recorded in Scotland, and a large chunk of those were recorded among the triple vaccinated population in the week ending 14th Jan 22, with 71 deaths.
In all the vaccinated population have accounted for 85% of all Covid-19 deaths since December 18th, with the triple vaccinated accounting for 50% of all deaths among the vaccinated population, and the double vaccinated population accounting for 44%.
Each week since 18th Dec has seen the double vaccinated population account for the most Covid-19 deaths, but the most recent week beginning 8th Jan 22 saw deaths among the triple vaccinated soar, as can be seen in the following chart.
The week beginning 8th Jan 22 saw the vaccinated account for 87% of all deaths, with the triple vaccinated accounting for 66% of deaths among the vaccinated.
In all between 25th Dec 21 and 21st Jan 22 the not-vaccinated population have accounted for 19% of hospitalisations, the one dose vaccinated have accounted for 5% of hospitalisations, the double vaccinated have accounted for 26% of hospitalisations, and the triple vaccinated have accounted for 49% of hospitalisations.
Whilst between 18th Dec and 14th Jan 22 the not-vaccinated population have accounted for 15% of deaths, the one dose vaccinated have accounted for 5% of deaths, the double vaccinated have accounted for 38% of deaths, and the triple vaccinated have accounted for 42% of deaths.
If you believe this is to be expected because a higher percentage of the population have been vaccinated then we’re sorry to have to tell you that you are very mistaken, because the hospitalisation and death rates per 100,000 individuals in Scotland have also been highest among the fully vaccinated population over the past month.

These figures therefore suggest the vaccinated are suffering antibody-dependent enhancement, and we’ve gone into great detail on the rates per 100,000 figures in an article you can read here.
Wednesday 26 January 2022
Virus Destruction by Resonance
Very interesting paper on the Rife machine
Source:
https://www.scirp.org/journal/paperinformation.aspx?paperid=106157
Viruses and other microbes can be inactivated in a selective way by subjecting them to an oscillating electric field of adequate frequency. Royal R. Rife discovered this method already about 100 years ago. He proved its efficiency by means of high resolution microscopes and in 1934, by controlled clinically tests. However, these results seemed to be unbelievable, since the underlying mechanism was not yet understood. Actually, we are faced with three problems: 1) the functioning of Rife’s supermicroscopes, 2) his observation that bacteria can undergo size reduction, and 3) the decisive resonance phenomenon. We explain the high magnification and resolving power of Rife’s microscopes and show that new discoveries confirm that the postulate of invariable forms of bacteria has to be abandoned. Then we prove that forced oscillations of virus spikes lead to a peculiar resonance, because of nonlinear effects. It causes total destruction of the virus by rupture of its coating. The same theory applies to bacteria and nanobacteria, because of their pili. The worldwide coronavirus pandemic, the constant threat of unpredictable mutations and the now available explanations should make it obvious that biophysical methods cannot be neglected anymore.
Share and Cite: Meessen, A. (2020) Virus Destruction by Resonance. Journal of Modern Physics, 11, 2011-2052. doi: 10.4236/jmp.2020.1112128.
Royal Raymond Rife (1888-1971) was an outstanding scientific inventor, who wanted to help humanity by discovering and fighting still unknown causes of sickness and death. His achievements and the opposition that he encountered were described in the remarkable book of Barry Lynes [1]. In his youth, Rife had been impressed by the discoveries of Louis Pasteur and Robert Koch during the second half of the 19th century. They used microscopesto see lethal microbes. They could then isolate and culture them. When the resulting entities caused always the same sickness after repeated cycles, the next step was to find specific vaccines to help their recognition by our immune system. Rife suspected that cancer does also result from microbes, but that they are too small to be seen by means of standard optical microscopes.
This limitation results from the wave nature of light. It leads to interference effects. The physicist Ernst Abbe, working for the Carl Zeiss Company, established even in 1873 a relation between the best possible resolving power of optical microscopes and the wavelength of light. It is at best of about λ/3, where λ is the wave length for visible light. The limit is thus about 180 nm, but for ultra violet light, λ < 400 nm. The Carl Zeiss Company developed therefore UV fluorescence microscopes. The light source was an intense electric arc lamp and the UV light was concentrated on the specimen by means of quartz lenses. Since the specimen converted this light by fluorescence into visible light, the objective and ocular were glass lenses. In 1913, the Carl Zeiss Company was ready to sell this new type of microscopes [2].
Rife started in 1917 to construct himself a better microscope for visible light and finished it in 1922 [1]. It magnified up to 17,000 times, while the best standard optical microscopes could only reach 2000 - 2500 times. Moreover, the images were well-contrasted, with unprecedented high resolution. How this was achieved remained an unsolved puzzle. Rife constructed even more powerful optical microscopes. His second one was finished in 1929 and the third one in 1933. He called it a “universal microscope”, because of its great adaptability. It could even magnify up to 60,000 times.
These supermicroscopes allowed him to make extraordinary discoveries, but they contradicted the beliefs of medical authorities. Using only conventional microscopes, they were unable to observe what Rife saw by means of his supermicroscopes. Moreover, Rife discovered the cancer microbe, although it was generally assumed that cancer is not an infectious sickness. Science progresses, of course, by discovering previously unknown facts and by explaining them, but that may require correcting previous assumptions. Unfortunately, it is very difficult to modify deeply rooted ideas. One objective of this article is to illustrate this fact by analyzing Rife’s discoveries and achievements, to show the complementarity of experimental and theoretical methods.
It has been claimed [3], for instance, that it is impossible to reach the high resolution of Rife’s microscope, by repeating the standard theory. It is also incorrect to believe that Rife did suppress the interference effects [4]. The Nobel Prize in Chemistry of 2014 was actually awarded for the development of super-resolved microscopy [5]. This was achieved by using powerful lasers, while Rife succeeded with purely classical means. Nevertheless, his name has been wiped out from official medical and scientific literature.
Fortunately, some documents were preserved and their analysis did help us to uncover the secret that escaped attention. Moreover, they provide first-hand information about the discoveries that Rife made with his new microscope. The first one concerned the existence of “nanobacteria”, resulting from size-reduction of known bacteria. They are more virulent, but Rife discovered also a method to destroy them, by resonance. To observe both phenomena very clearly, he constructed the more powerful microscopes. The size of typical bacteria is of the order of 1000 nm. For viruses, it ranges from about 400 to 20 nm, but their existence had already been established at about 1900 by means of porcelain filters with very narrow pores. The filtrate contained no bacteria, but remained virulent. This fact justified Rife’s conviction that these mysterious entities should be observable by means of better microscopes.
A description of his universal microscope was published in 1944 by a scientific journal [6]. It mentioned also other new optical microscopes and compared them with electron microscopes, developed in the 1930th. Their magnification is greater and allows for instance to determine the size of the polio virus. It is merely 30 nm. The diameter of the spherical core of the Covid-19 virus is 85 nm and it carries 20 nm long spikes. However, electron microscopes can only yield images of dead microbes. The article of 1944 insisted thus on the “great interest” of the new type of optical microscopes, since they allow scientists to penetrate the unseen world of the minute and disease-causing organism when they are still living and active.
This was essential for Rife, but how did he acquire the competence for his apparently impossible achievements? We know that he began medical studies in 1905 at John Hopkins University in Maryland, but he broke them off. His aim was to construct as soon as possible a better microscope and to find the cancer microbe. It has been reported [7] that he married in 1912 and moved then to San Diego, California. Speaking German, he travelled often before WWI to Germany for the US Navy. Rife provided himself reliable information in 1960, by answering 137 questions of the lawyer of his collaborator John Crane [8]. He was on trial, since the powerful American Medical Association (AMA) had decided to abolish the Rife/Crane cancer therapy. It was declared to be bogus, even without examining Rife’s methods and results. After Rife’s trial, orchestrated already in 1939 by AMA, he was forced to stop his research. He was bankrupt and desperate. His laboratory had been raided. His microscopes were made unusable and documents were stolen. They included also movies of the behavior of the tiny living beings that Rife made visible. He took refuge in Mexico. Even his written answers of 1960 were not allowed to appear in court during Crane’s trial in 1961, but they were conserved.
Rife’s answered (to question Q.38) that he acquired his expertise in optics by working for 6 years with Hans Lukel, who was Carl Zeiss’s scientist in the USA. Rife mentions there also that he made “all the photomicrographs for the Atlas of Parasites which was done at the University of Heidelberg”. This book was published in 1914 and contained more than thirteen hundred colored lithographs [9]. Our inquiries at the archives of the universities of Heidelberg and Gießen, as well as at the Carl Zeiss History Support in Jena revealed no recorded or easily accessible traces. The authors of the book did only thank their academic colleagues. Anyway, it took nine years before Rife felt ready to begin his own research (Q.39). The link [8] provides photographs of his microscopes and the copy of a certificate, where the Institute for Scientific Research of the Andean Anthropological Expedition recognized Rife’s “outstanding contributions to science” and the attribution of a Research Fellowship in biochemistry. Rife confirmed this (Q.135-137) and added that he studied bacteriology at John Hopkins University (Q.56). He acquired there a PhD diploma, since he signed a scientific paper [10] with this title and was often called Dr. Rife.
When he was running out of financial resources, he took a job as chauffeur of the multi-millionaire Henry Timken. He manufactured ball bearings and Rife provided a way to control their quality by constructing an X-ray machine. Timken valued his creativity and technical abilities, demonstrated in various ways. Impressed by Rife’s competence and his strong motivation to construct better microscopes for identifying the cancer microbe, Timken offered him a laboratory at Point Loma, California, with full equipment and financial support.
Rife constructed there his microscopes and the basement provided facilities for 1000 animals with precisely controlled air-conditioning (Q.10). There were about 800 albino rats, but also Guinea pigs and rabbits (Q.59). In 1929, a local newspaper published an article about Rife’s extraordinary microscope and his fascinating discoveries [11]. The journalist praised his competence in bacteriology, chemistry, metallurgy and engineering. Rife had developed methods to observe and document previously unobservable living entities. He found even a technique to destroy harmful microbes, but “refuses to make money from it”. He is concerned with pure science and wants to free humanity from cancer and other dreadful sicknesses.
In his interview [8], Rife provides important details concerning his research and the difficulties that he encountered. He did use cancer tissues and prepared over 15,000 slides, since he was convinced that his microscope should allow him to see the microbe that causes cancer, but it remained hidden. He tried numerous molecules for staining and this lasted over 10 years, to no avail (Q.22). Eventually, he thought that chemical substances might destroy the mini-microbes and started therefore to exploit other capabilities of his microscope. Although this was time-consuming, it allowed him to select a color that made microbes visible by their own luminescence, without having to add some staining substance. It was also necessary to discover a method for multiplying the microbes that he expected to be present in cancer tissue. He found that they had to be cultured in the “K medium”, developed by the microbiologist Arthur Kendall. This medium is protein based, but poor in peptones (polypeptides and amino acids). It was superior to all other ones (Q.29 and 30). Nevertheless, the decisive breakthrough was quasi-accidental [12].
“After many long procedures and unsuccessful attempts”, Rife had fortuitously placed a test tube near an argon discharge tube. It ionizes air and produces
The culprit of cancer or at least a new possible cause had thus been uncovered. It was a tiny ovoid particle, about 50 nm large and 70 nm long. Its motility indicated that it was flagellated [10]. Rife observed also with his supermicroscope that these BX entities could be transformed again into bacteria or fungi, according to the medium where they were living. In their reduced form, they could not be destroyed by UV radiation or X-rays, but they were killed after two days at 42˚C. The newspaper article [11] attracted the attention of Dr. Arthur Kendall,whohad developed the K medium. He was professor and head of the department of bacteriology at the Northwestern University in Chicago and wanted to check the reality of these amazing claims.
He invited Rife in 1931 to bring his microscope to his institution, where he used a type of bacteria that he had cultured himself. In their “filterable state”, they appeared in Rife’s scope as tiny, motile granules of turquoise-blue color. These observations were so astonishing, that the whole procedure was repeated eight times. In 1931, Prof. Dr. Kendall published with Rife an article [10] that described these experiments and their results. Kendall was then invited to speak in 1932 at a meeting of the Association of American Physicians. Dr. Thomas Rivers, virologist at the Rockefeller Foundation, tried to get Kendall’s talk cancelled. This was not accepted, but Rivers went immediately to the podium after his talk to express fierce opposition. He impressed the audience by daring to address Dr. Kendall as if he were a liar.
Dr. Rivers and Dr. Zinser, bacteriologist at Harvard, had tried to reproduce Kendall’s results. They did use the K-medium, but their observations were made with conventional optical microscopes. Without Rife’s supermicroscope and his method to provoke luminescence, they were unable to see the relevant nanoparticles. Moreover, they believed in monomorphism, advocated by Louis Pasteur. He had attributed infectious diseases to bacteria of specific size and form. A similar postulate is used for classifications in botany and zoology, but metamorphosis is not impossible. Since Rife and Kendall were facing ideology, Dr. Edward Rosenow, who was heading the Mayo Foundation's Experimental Bacteriology program at Rochester, Minnesota, wanted to check the facts. He spent 3 days at Kendall’s laboratory where Rife’s microscope was still installed and reported his observations in Science [13]. He wrote: “there can be no question of the existence of filterable turquoise blue bodies”. They appear in large numbers in filtrates of cultures of infected tissues and constitute a “stage in the development of microorganisms.”
Rife mentioned in his interview [8] that the BX entities are actively moving around (Q. 51), but that he found a method to “devitalize all microorganisms as desired” (Q.19). It required EM waves of particular frequency, depending on the kind of microbes. This frequency was determined by observing the microbes with his microscope (Q.76). Some types did then “explode or disintegrate” and other types did aggregate (Q.80). This happened for various types of bacteria (Q.78), but they were never affected by inadequate frequencies (Q.118). This observation led to the development of the “ray machine”. Its production was continued by John Crane when Rife fled to Mexico, but Crane was prosecuted. AMA accused him, though it refused to test his system (Q.131). The American Cancer Society was interested, until they found out that Crane and Rife were not medical doctors (Q.127).
However, Dr. Milbank Johnson, Professor of Physiology and Clinical Medicine at the University of Southern California, gathered in 1934 a Research Committee to test the clinical efficiency of Rife’s cancer therapy. Sixteen terminally ill patients with different types of malignancies were selected and treated with the instrument that produced an oscillating electric field of the required frequency for deactivating the BX entities. The sessions lasted only 3minutes,every third day. The patients felt neither pain nor any other sensation, but “the virus or bacteria is destroyed and the body then recovers itself” [1]. The interval between treatments was needed to eliminate the toxic debris. “After 3 months, 14 of these hopeless cases were signed off as clinically cured by the staff of five medical doctors”. Other ones participated in overviewing this test and the pathologist of the group, Dr. Foord, certified the healing. The two other patients were cured after 20 more days [7]. The first cancer clinic that used the Rife technology was opened in 1934 and the Rife Beam Ray Company was operating in 1938. That was intolerable for the powerful AMA. The capitalistic pharma industry wanted also to prevent the development of alternative forms of medical treatments, of course, but had merely to encourage AMA’s request of legal prohibition and its use of other methods of coercion. This procedure has been analyzed in the context of social anthropology, related to science and technology [14]. It is necessary, indeed, to realize that it was profoundly unjust, unscientific and even harmful, by preventing possible cure.
The structure of this article results from the need to solve three basic problems. Section 2 describes Rife’s supermicroscope and explains its functioning. Section 3 justifies the concept of pleomorphism. Section 4 provides a detailed scientific explanation of the physical mechanism of targeted microbe destruction by resonance. This part illustrates also the usefulness of physical reasoning for solving scientific riddles, even in medicine. Section 5 presents conclusions and some recommendations.
2.1. Rife’s Universal Microscope
The basic principles of microscopy result from the laws of geometrical optics. All light rays that emerge from a point A and pass through a lens L do converge at the point A’. To determine its position, it is sufficient to consider two rays, as shown in Figure 1. The ray that passes through the center of a thin lens is not deviated, while the ray passing through the focal point F is refracted by the lens to become parallel to its symmetry axis. This applies even to combinations of thin lenses. The position of the image A’ of A is determined by 5 parameters: their distances D andd from the plane of the lens, their heights H and h above and below the symmetry axis, as well as the focal lengthf of the lens L. Indeed,
Analogous relations apply to the second lens L’. Since the rays that emerge from A’ and pass through this lens are refracted as if they did emerge from I, this is a virtual image. The global magnification is the product of the magnifications provided by the objective and ocular lenses.
Rife modified this system to get a much greater magnification by increasing the distance D. He did that by intercalating many prisms as indicated in Figure 2. We represent there only a narrow bundle of rays, forming a beam that would coincide with the symmetry axis if it were not deviated. Rife stated in his description [15] that the beam was subjected to “21 light bends”. There are only 20
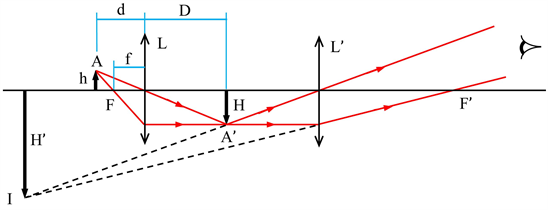
Figure 1. Successive formation of two images A’ and I of the point A in optical microscopes.

Figure 2. Rife achieved great magnification by increasing the distance D between the lens L and A’.
prisms, but the image A’ does also produce a deviation to yield the image I. Rife insisted that the rays of light have to remain nearly parallel, although the rays emerging from the lens L are converging. The 90˚ prisms did thus not simply act like mirrors. One of their faces was slightly concave. Every time before the rays would tend to meet, they were thus made less convergent. This stratagem required extremely high precision, since the total deviation from the ideal one could not exceed one wavelength.
The distance that light rays traveled zigzag fashion was 449 mm, while the length of the barrel was only 229 mm. For usual microscopes it is 160 - 190 mm. All prisms and lenses were made of block-crystal quartz. The barrel and screws were made of “magnalium”. This AL/Mg alloy was very expensive, but it has the same thermal dilatation coefficient as quartz. Figure 1 shows that both focal distances f and f' should be as small as possible. Rife opted thus for a pair of identical, high-quality objectives with quartz lenses, developed by Zeiss. Why did Rife not follow the contemporary trend to improve resolution by using UV light? It would not be converted everywhere into visual light when it passes through the specimen, but is dangerous for visual observation. Though it could be eliminated by a filter, Rife preferred to use a normal light source, since his initial intention was to use chemical staining.
Rife knew that molecular fluorescence results from processes that are represented in Figure 3(a). The curves show how the energy E depends for the ground state and the first excited state on the structure parameter s. Photons of blue or near ultraviolet light can thus excite an electron from the most probable ground state to another possible state. The molecule modifies then its configuration before emitting a photon of lower energy. Since absorption and emission of a photon are instantaneous processes, they are represented by vertical transitions. There are also vibrational states, leading to spectral bands instead of lines, but we can simplify the graph, since the essential point is that molecules, which can rapidly lose any excess energy. However, it was necessary that the light source could provide light of any required color to elicit optimal fluorescence.
An electric arc is a very intense light source, but there are spectral lines. Rife preferred thus an incandescent filament. It yields a continuous spectrum and Rife did use a special filter to select the adequate color. It had been invented in 1889 by the ophthalmologist Risley and is represented in Figure 3(b). Indeed,

Figure 3. (a) Molecular luminescence is optimal when it is excited by light of a particular color. (b) It was selected by a Risley filter. (c) Rife’s secret was a pinpoint filter near A’.
two identical 90˚ prisms can be rotated with respect to one another, while their oblique faces remain in contact. At normal incidence light is only refracted at the interface. This leads to dispersion, but by rotating the prisms with respect to one another, we get only light of a particular color that leaves the second prism at normal incidence. Since quartz is birefringent, the angle of refraction depends not only on the color, but also on the polarization of light waves. Rife could thus produce polarized light of any desired color. This is useful for mineralogy, since thin slices reveal then colored parts.
Figure 3(c) represents the pinpoint filter that Rife did place before the first image A’, but he did not mention it in his dialogue with Crane [16]. He stated there (#43) that the universal microscope has “a resolution of 31,000 times and a magnification of 60,000 times”. These values have often been repeated, without explaining how they were determined, but Rife mentioned that he used a Zeiss silver coated slide, carrying 800 lines per mm with perfect definition. They were thus separated by 1.25 μm. Under a standard microscope, there appeared 40 - 60 of these lines with distortions, due to spherical aberration of the lenses. “Under the universal microscope, we see only 1 - 3 lines and they are perfectly parallel through the entire field” (#44 and 45). The greater magnification kept only the central part of usual images. Rife claimed that “the resolution is 31,000 times”, which is unusual, but he considered that the sharpness of the image reached at least half the separation of the lines.
The high resolution remained very puzzling, since Feynman noted in his famous lectures on physics (I, 27-7) that we might build a “system of lenses that magnifies 10,000 diameters, but we still could not see two points that are too close together.” We mentioned already that the resolving power of optical microscopes is limited by interference effects. However, Rife answered only to Cranes question concerning this limit (#43) that the lack of sharpness is due to “factors of error that come into the field of optics by the illumination and things of all sort.” The use of a pinpoint filter just before the first image was not mentioned. Even in the article of 1944, Rife noted merely [6] that “if one pierces a black strip of paper or cardboard with the point of a needle and then brings the card up close to the eye so that the hole is in the optic axis, a small brilliantly lighted object will appear larger and clearer, revealing more fine detail.” This hint has not been perceived, but Rife’s method is equivalent to a recent discovery [5], that deserved even a Nobel prize.
2.2. Modern High-Resolution Microscopes and Diffraction
Stephan Hell, who pioneered the use of lasers for high resolution optical microscopy, explained the basic idea in his Nobel lecture [16]. He began with underlining the advantage of minimally invasive optical microscopy with respect to electronic microscopy. However, the resolution of optical microscopes is limited and “scientists believed throughout the 20th century” that this barrier cannot be overcome”. Knowledge of Rife’s achievement had been wiped out, but Hell thought that “so much new phenomena were discovered” that higher resolution of optical microscopes should be realizable. He was teaching biophysical chemistry in Göttingen and attributed the difficulty to the fact that light is emitted by different molecules inside a small volume of the specimen. They are exited together and emit light by the molecular processes that were depicted in Figure 3(a). Since it is impossible to excite only a very small group of molecules, he tried to find out if we can “manage to keep some molecules dark”.
Searching an answer to this question, he found that physics knows about stimulated emission of radiation. Einstein discovered this phenomenon in 1917 by proving that it accounts for Planck’s spectrum of EM radiation in an oven or any cavity at sufficiently high temperature. With lasers, it is possible to silence excited molecules by “stimulated emission depletion” (STED). This process is represented in a simplified way in Figure 4(a). Blue laser light (1) of moderate intensity is absorbed by a molecule. An electron is there raised from the ground state So to the first excited state S1. The molecule relaxes, by changing its configuration. The interrupted line represents this loss of energy, since it is sufficient to represent the initial and final excited state to account for Figure 3(a). Light emission result from the transition (2) in Figure 4(a), but stimulated emission (2’) can be caused by intense laser light of the adequate frequency. The excited state is then constantly emptied and normal light emission is quenched.
Figure 4(b) represents the spatial domains of illumination by means of the two lasers. These light distributions cannot be point-like, but it is possible to produce a blob of blue light (1) and to superpose a ring of very intense green light (2’). It abolishes light emission in this ring and leaves only the small central spot where light emission (2) is still possible.
Once the spell was broken, other scientists did tackle the same problem during the two last decades and discovered various methods to solve it. They were reviewed in a comprehensive and interesting way [17]. The basic technique consisted always in separating light emission in space or time. How could Rife succeed already in the 1920th to reach high resolution without lasers? To understand this fact, it is useful to return to basics.
Grimaldi’s careful observation in 1660 of the shadow cast by a rod revealed that it cannot be explained by geometrical optics, unless light rays that pass close to obstacles are divided (at least) in two rays. This led to the concept of “diffraction”.

Figure 4. (a) Transitions between energy levels, used for high-resolution microscopy by the method of stimulated emission depletion (STEP). (b) Superposed illuminations and the resulting emission.
Grimaldi thought already that light may not be constituted of particles that are moving along straight lines in any homogeneous medium. Young’s famous double slit experiment of 1801 proved that light is propagating like waves. It was then generally believed that there are “light waves”, but Planck discovered in 1900 that there are grains of light energy and Einstein proved in 1905 that they are particles. These photons do not always move along a single well-defined trajectory, but do also allow for interference.
In 1815, Fraunhofer discovered spectral lines in sunlight by improving the quality of lenses and prisms, but he did also use gratings with many equidistant narrow slits. The resulting interference decomposes white light in different colors. Fraunhofer found that a single slit produces also a set of closely spaced interference fringes. Even when light encounters a screen with a small circular hole of radius r, as shown in Figure 5(a), it does produce a brilliant spot of light that is surrounded by fainter rings. Fresnel explained this fact in 1819 by considering that all points inside this hole emit spherical light waves, but on the symmetry axis, they do always interfere constructively with one another. Figure 5(b) shows that for the angle θ with respect to the symmetry axis, light emitted by any pair of points that are radially separated by the distance r interferes destructively for monochromatic light of given wavelength λ, when
For other angles the wave amplitudes are not opposite to one another. Fresnel calculated the resulting variation of the light intensity and found that it varies as indicated in Figure 5(c). It is even the square of a Bessel function. The arrows define the width of the central spot, resulting from relation (2).
Distant stars are point-like light sources, but for telescopes, their image is a spot of light that is surrounded by rings of decreasing intensity. This was proven in 1835 and led to the term “Airy disc”. It is represented in Figure 6(a), when light intensities are represented in black/white inversion. Figure 6(b) recalls that all light rays that emerge from the point A and pass through the lens L will converge at the point A’. Ernst Abbe realized in 1873 that a microscope is thus equivalent to a circular hole of radius
Figure 5. (a) Light passing through a small circular opening leads to interference. (b) It is always destructive for a particular angle θ. (c) The angular distribution of the resulting light intensity I yields a central blob, surrounded by fainter luminous rings.
Figure 6. (a) Black/white image of an Airy disc. (b) Formation of the first image in a microscope. (c) The resolving power r defines the smallest distance between separable point-like sources.
The value of r results from (2) and the fact that light rays are refracted by the lens. NA is called the “numerical aperture” of the lens system, since it depends on the angular opening θ of the diaphragm and the index of refraction n of the medium between the specimen and the lens. It refracts light wave, but on the other side of the lens L there is air, where n = 1. Figure 6(c) shows that the blurred image of two points near A can only be separated when their separation is greater than r. The resolving power of microscopes is thus defined by (3). Abbe concluded that the resolution of optical microscopes can be improved by filling the space between the sample and the lens with a transparent fluid, where n ≈ 1.5. Immersion does thus reduce r from λ/2 to λ/3.
2.3. Rife’s Method and Other Supermicroscopes
It has been asserted [3] that Rife could not overcome the diffraction barrier and that he did suppress it by applying the principle of reversibility [4]. Sorry, this principle is only valid in geometrical optics, since it implies that the direction of propagation of light is irrelevant for light rays. Diffraction of light that passes through a small circular hole or a narrow slit results from interference and cannot be eliminated, but Figure 4 showed that the difficulty can be bypassed. How could Rife also do that without lasers?
Rife’s contact with the Zeiss Company and his own observations made him aware of diffraction phenomena, but he found a very simple way to reduce their effects. He combined very high magnification with a pinpoint filter, which reduces the size of the Airy disc at A’, as shown in Figure 3(c). Probably, Rife did not mention this filter to protect his invention. It is even impossible to verify that he did use a pinhole filter, since his microscopes were dismantled. Rife constructed in 1932 a supermicroscope for a friend, who was a watchmaker and may have given advice for high precision tooling. This instrument was sold on auction in 2009, but the objective and ocular lens systems were missing, as well as the pinpoint filter [18].
It is very remarkable that Gaston Naessens (1924-2018) developed in 1949 another type of optical supermicroscopes with specialists of the Leitz Company in Wetzlar, Germany. This instrument reached a magnification of 30,000 and a sufficiently high resolution to see very small living entities. Naessens called them “somatides” and his microscope a “somatoscope”. He observed that these somatides resulted from changes of size and form of normal bacteria. They could pass through a simple or a complex life-cycle [19]. This is demonstrated in a short and very interesting video [20]. His microscope was also based on bioluminescence, but the exciting radiation was very intense UV and blue light of fixed wavelengths, respectively of 185 nm and 330 nm. Since excitation like that of Figure 3(a) requires a specific color, this was achieved by means of magnetic and electric fields, modifying molecular spectra in an adaptable way.
Since we ignore if he did also use a pinhole filter to achieve very high resolution, we wonder if other methods might have been used. This is conceivable, since Figure 7(a) accounts for excitation by means of UV light that allows for transitions (1) between the ground state So and a higher exited state S2. The energy is then reduced, by modifying the configuration parameter s of the molecule. However, the curve S2(s) cuts the curve S1(s). The exited electron goes then over to the lower energy state, which allows for immediate light emission (2), called fluorescence.However, the excited electron can also go over from S1 to another state T. It is a triplet state, since the spin of the excited electron has been reversed. We get thus an electron pair, where the total spin is 1 instead of 0 for singlet S states and the transition T → So is forbidden. The electron is thus trapped until it is thermally excited to reach again the level S1. This allows for retarded light emission, known as phosphorescence.Since there is no fixed phase relation anymore with the exciting light, the emitted light waves are incoherent and cannot interfere.
Another method consists in placing a pinpoint filter precisely at the point A’, as shown in Figure 7(b). This has mainly the advantage of improving depth sharpness, since light emerging from other planes than at A will not be focalized in the image plane A’. This type of confocal microscopy was invented and patented in the 1950th [21]. It allowed for laser scanning. Optical microscopy made thus remarkable progress, but the pioneers, Rife and Naessens were unjustly discarded from the list of honorable scientists.
They did use their microscopes for observing that bacteria can reduce their size and developed then methods for fighting sicknesses. Rife did this by resonance and Naessens by discovering drugs that he could observe to be efficient, but he was prosecuted for illegal exercise of medicine [22]. Rife and Naessens did not belong to the required corporation or caste. This mentality is akin to racism,since it was not even deemed necessary to check if their observations were correct and if their treatments were helpful or not.
Figure 7. (a) Excitation of fluorescence and phosphorescence. (b) Confocal microscopy.
3. Biological Discoveries and Medical Applications
3.1. Pleomorphism Revisited
Antoine Béchamp, a compatriot of Pasteur, proved already by extensive experimentation that the size and form of bacteria can be modified [23]. He introduced the term pleomorphism,meaning more possible forms.He found that the smaller entities survive in chalk, but can reacquire their usual size and even become fungi. In 1886, Béchamp described “microzymas” (small ferments) that subsist as living entities after the death of organs, although it was believed that nothing can survive. These microzymas can also be present in living beings, where they cause diseases, but Pasteur did fiercely defend his conviction that all infectious diseases are only due to microbes of external origin. Béchamp was doctor of pharmacy and professor of chemistry. He became a medical doctor and then professor of medicine. He was a member of the French Academy, like Louis Pasteur, who was a chemist. Pasteur made very important discoveries, but was quite intolerant. He had even a feud with Robert Koch [24] and reacted so aggressively against Béchamp that monomorphism prevailed by docile consent of colleagues.
Nevertheless, Mrs. Henri of the Pasteur Institute in Paris observed in 1914 that anthrax bacilli change their form when they are subjected to ultraviolet light [25]. Monomorphism was also contested by the Swedish Biologist Ernest Almquist [26]. He wrote in 1922: “Nobody can pretend to know the complete life cycle and all the varieties of even a single bacterial species. It would be an assumption to think so.”
Rife was not aware of these controversies or not interested. His aim was to observe the tiny microbes that he expected to exist. He succeeded and found even that “any alteration of artificial media (for culturing bacteria) or slight metabolic variation in tissues will induce an organism of one group to change over into any other organism included in that same group”. These transformations are reversible, but the bacillus typhosus yields always turquoise-blue luminescent entities. For the bacillus coli it has a mahogany color, for tuberculosis it is emerald green and for the BX purplish-red.
Rife found that inoffensive bacteria become virulent when their size is reduced. He thought therefore that bacteria do not produce themselves diseases, but the microorganisms that result from their transformation. “If the metabolism of the human body is perfectly balanced or poised, it is susceptible to no disease”. Rife added nine years later [12]: “with a pure culture of bacillus coli, by altering the media as little as two parts per million by volume, we can change that organism in 36 hours”. In the initial medium, the micro-organism becomes again a bacillus coli. Continued microscopic study and stop motion photography confirmed the reversibility and revealed that the BX allows for “many changes and cycles.”
In experimental animals, the BX produces “a typical tumor with all the pathology of true neoplastic tissue, from which we can again recover the BX micro-organism”. They are even abundantly present. To be absolutely sure of this astounding result, Rife repeated these observations several hundred times. It should be noted that he tended to use the term “virus” for any type of filterable microbes, since the specific mode of virus reproduction was not yet known. The biologist Gaston Naessens observed pleomorphism in more detail. He presented clear evidence in a video [27] that the somatid found in blood can have a simple lifecycle or one with 16 different stages. Can these facts simply be negated, since they are not observable with standard optical microscopes? The books of Lynes [1] and Bird [23] denounce the enormous lack of scientific honesty in regard to the discoveries of Rife and Naessens.
Fortunately, it is possible to rediscover what is happening in Nature. Emmy Klieneberger-Nobel published in 1951 a thorough study of filterable forms of bacteria. She used a phase-contrast microscope, developed in 1942. It converts subtle phase changes of light waves passing through the specimen into amplitude modifications. They are made perceptible by reducing the amplitude of the background waves. This method made it possible to discover reversible changes of various types of bacteria, resulting from modifications of their environment [28]. According to her long list of references, she was not aware of the discoveries of Rife and Naessens, but the reality of pleomorphism was confirmed.
Kurath and Morita demonstrated in 1983 that marine bacteria are able to adapt themselves for survival under conditions of nutrient starvation [29]. The geologist Robert Folk discovered in the early 90th that precipitation of carbonates in hot springs of central Italy is due to modified bacteria. He studied them by scanning electron microscopy (SEM), proving that heir average size was 200 nm. In 1994, Folk attributed the observed carbonate precipitation to negatively charged cell walls. They attract Ca++ ions, neutralized by CO3 ions, which yields chalk (CaCO3) [30].
Kajander and Ciftcioglu proved in 1998 that blood can contain nanobacteria, associated with Ca++, CO3 and PO4 [31]. Nanobacteria act then as crystallization centers that lead to the formation of kidney stones. The calcified envelope seems to provide a shelter for survival, since SEM micrographs revealed that they are still able of division. It appeared also that these nanobacteria are covered with a “hairy layer”. Transmission electron microscopy (TEM) confirmed the existence of this coat of mineralized whiskers.
However, the existence of nanobacteria raised controversies, since it was generally believed that bacteria have to be big enough to accommodate DNA or RNA, as well as the required enzymes for autonomous replication. The opposition to the concept of pleomorphism resurged, but now because of molecular genetics. Ciftcioglu, Kajander et al. responded in 2006 by more facts: pathological calcification caused by nanobacteria does also account for gallstones, arterial heart disease, prostatitis, cancer and Alzheimer’s disease [32]. They stated that research in this area has been “paralyzed for decades by attributing the calcifications to insignificant, passive, degenerative processes of aging”.
The dermatologist Milton Wainwright published already in 1990 a book [33], where he presented important results concerning microbiological causes of cancer. He discovered that scleroderma, a rare form of cancer that leads to hardening of the skin and inevitably to death, is caused by microbes. Other outstanding physicians and medical research scientists had also demonstrated in the meantime that various forms of cancer result from nanobacteria, but the medical establishment did recklessly reject all proofs that contradicted the standard dogma. Wainwright’s book of 2005 provides ample proof of this kind of “medical politics” [34].
Milton Wainwright recalled the battle between pleomorphism and monomorphism [35], since it is still going on. By dismissing this possibility, “we may be missing something of fundamental importance”. A review [36] concluded in 2011 that “the evidence that nanobacteria exist in the human body and are closely associated with many kinds of diseases is now overwhelming”. Nevertheless, it came still in 2011 to a categorical denial [37]. It refereed unjustly to a study of Ciftcioglu and McKay [38]. It was much more careful and mentioned that calcifying nanoparticles “do not fit the typical definition of life”, but it could be too restrictive. Smaller forms have detrimental effects on human health and should be the “focus of future effort.”
Cantwell insisted again in 2014 on existing evidence that cancer is caused by pleomorphic bacteria [39]. More and more justifications of the relevance of modified forms of bacteria in human pathologies have been published. Russian scientists presented in 2012 a review [40] where coccoid nanobacteria were reported to appear in sea water, soil, sedimentary and granite rocks, the Greenland ice sheet, glaciers and permafrost soils, as well as in humans and insects, for instance. Their size can be reduced to about 150 nm. This article contains several micrographs showing that ultramicrobacteria can make contact with one another by means of hair-like appendices. Banfield’s team at the University of California, Berkeley, collected nanobacteria by filtering acetate-amended ground water [41]. These cells were immediately deep-frozen to prevent deterioration and brought to the laboratory, where they were analyzed by CryoTEM. It appeared that these nanobacteria are even quite common and well-adapted for survival under adverse conditions. A widely published micrograph [42] shows a coated spherical particle. Its diameter is close to 300 nm and its surface is covered with numerous pili, radiating outwards. Their length is about 50 nm. Their presence attracted our attention and will turn out to be very important.
Lida Mattman was an outstanding microbiologist. She confirmed pleomorphism and described the life cycle of various bacteria. Her textbook [43] concentrated on “cell wall deficient forms”. They could result from an adaptation to increase protection against natural antibiotics, but they remained hidden in blood, though they are damaging. “Current bacteriology holds the belief that each cell species has only one simple form and retains it by reproduction”. Nevertheless, they are able to “pass through stages with markedly different morphologies”.
Dennis Claessen and his group at the Institute of Biology in Leiden discovered filamentous bacteria that are present in soils. He called them “actinomycetes”. In response to stress, they can become cell wall deficient [44]. This may be a transient state, but also a lasting one. Pr. Claessen commented in an interview: “It gives a whole new understanding of the flexibility of microorganisms under stress and their ability to adapt to their environment.” He published an article in 2019, where he reviewed recent progress concerning stress induced wall deficiency and pleomorphism [45]. He concluded that during the last decade, it became increasingly clear that “cells have a wide range of defense mechanisms to cope with various stresses.” This is also clinically relevant, since morphological plasticity can cause reinfections.
It is particularly noteworthy that Rife discovered that deadly nanobacteria did thrive in tissues that had been treated by α, β and γ radiation or cobalt 60 gamma rays [46]. The idea that cancer results only from mutations, due to radiation damage and some chemical substances, needs revision, since we were not aware of pleomorphism, caused by stress.
3.2. Rife’s Method for Producing EM Waves
His aim was not only to see small microbes, causing sicknesses and death, but also to destroy them. He suspected already 1915 that this might be possible by subjecting them to oscillating electric fields. He declared [8] that systematic experimentation started in 1920. At that time radio amateurs were very active. The carrier wave for radio frequencies had initially been produced by means of a sequence of sparks (in German: Funken, meaning also radio-emission). The sparks result from high tension, obtained by means of a Ruhmkorf induction coil and an interrupter. The electric field accelerates some stray electrons that become then able to ionize air molecules. This produces more free electrons in avalanche fashion, but recombination processes lead to a spark and rapid discharge. This is also relevant for lightning.
When it was realized that electrons can be emitted by a hot filament, it became possible to fabricate luminous diodes. However, Lee De Forest used a vacuum tube and invented the triode, where the amplified electron flux can be controlled. This “audion” could thus modulate a high frequency carrier wave at audio frequencies and was patented in 1908. Public broadcasting began in 1922 from the Eifel tower in Paris and in 1926, NBC started radio emissions in the USA, but Dr. Rife wanted only to produce radio waves of limited range. Their frequency should be adaptable and stable to allow for selective action on particular microbes. Being technically gifted and very creative, he did that by combining two existing inventions.
On one hand, the German physicist and glassblower Geissler had created in 1857 a gas discharge tube, still used today as a source of colored light. It consists of a sealed glass vessel that contains a noble gas at low pressure and two electrodes. There is no hot filament, but a constant high potential difference is applied to these electrodes. The resulting field accelerates free electrons that will then ionize atoms. At low pressure, they are diffused by collisions before emitting light. The whole tube becomes thus luminous and the color depends on the chosen gas.
On the other hand, Coolidge invented in 1913 an X-ray tube that was a glass sphere. A hot filament emitted electrons, bundled and accelerated in high vacuum by a strong electric field to impact the other electrode at high velocity. They were there suddenly decelerated, but basic laws of electromagnetism predict that when the velocity of electrically charged particles is reduced, they emit braking radiation (Bremsstrahlung). Deceleration of high velocity electrons produces X-rays. Their frequency spectrum is continuous, but there are also superposed narrow peaks, resulting from excitation of strongly bound electrons inside atoms of the anode. They return to their normal state by emitting photons of particular energy. These processes yield a beam of X-rays that is emitted at 90˚ when the flat anode is inclined at 45˚ with respect to the electron beam. Rife created a new system, represented in Figure 8(a).
Actually, he replaced Geissler’s tube by a hand-sized glass sphere and the hot filament of the Coolidge sphere by a cold metal plate. When the applied potential difference between the two electrodes exceeds a particular value, there appears a glow discharge. It results from the fact that a local space charge is created near the negative electrode and pushes some ions towards the cathode. It emits then electrons that are accelerated and ionize atoms of the noble gas. Its pressure is such that diffusion of excited atoms is limited, but the accelerated electrons are constantly slowed down and hit the anode at moderate energy. Being suddenly stopped, they produce braking radiation, but the energy of the emitted photons is lower than for Coolidge’s X-ray tubes. The resultingbeam of radio waves is also perpendicular to the electron beam and represented by points in Figure 8(a). The lateral divergence of this beam is greater than for X-rays, because of the longer wave length.
The gas that surrounds the beam becomes luminous and such a diode is called a “phanotron”. Rife tried different noble gases. He found that helium is preferable, since the impact of the lighter He+ ions on the cathode increases its lifetime. Figure 8(b) indicates in a schematic way that the electric tension can be applied by modulating a signal of high-frequency F with rectangular pulses of lower
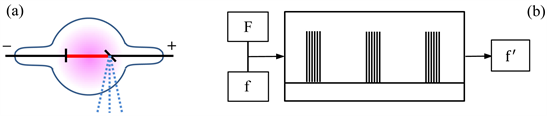
Figure 8. (a) Rife’s phanotron is a gas-discharge diode, where an electron beam produces at 90˚ a beam of EM waves. (b) An electric signal of fixed high frequency F is combined with pulses at a particular audio-frequency f to produce sinusoidal oscillations of desired frequencies f'.
frequency f. Since avalanche phenomena distort these signals, the resulting EM wave is equivalent to a superposition of sinusoidal waves of various frequencies f' by Fourier transformation.
3.3. The Rife Frequencies and Evidence of Exploding Microbes
The history of the development of Rife’s machine has been reconstructed in detail [47]. The report contains many photographs and includes new measurements. They were performed on rediscovered instruments or reconstructed ones, according to original schemes. This study was essentially concerned with engineering problems, but for us it is important that this system could produce electric fields that oscillate at any desired frequency f'. Rife provided a list of resonance frequencies for different types of microbes by observing their reaction with his microscope. Since they were definitively inactivated, he called them “mortal oscillatory rates”.
He communicated his initial list in 1935 to the electronic engineer Philip Hoyland. He had been hired by Dr. Milbank Johnson who operated a “cancer clinic” that used Rife’s method. Hoyland’s mission was to construct a more compact version of Rife’s machine. Electronics was constantly progressing, indeed. He determined also the resonance frequencies with Rife’s microscope and Rife did control his measurements. He agreed with the fine-trimmed values of 1936. Table 1 provides the carefully established list. It appears in the report (p.103), but is rearranged here for increasing frequencies instead of the names the pathologies in alphabetic order.
To produce these frequencies, Rife bought commercially available equipment of top quality. He needed a sinusoidal carrier wave of authorized frequency and was allowed to emit at F = 3,300,000 Hz. This signal, modulated by rectangular pulses, was fed to the phanotron. The pulses were distorted by avalanche effects and possible frequencies were then determined by
The numbers n and n' can be 1, ±2, ±3, … The sidebands have decreasing intensities for greater values of these numbers. Table 1 tells us that the resonance
Frequency | against | 549.07 kHz | Staphylococcus Albus |
139.20 kHz | Anthrax | 759.45 kHz | Typhoid Fever (rod) |
191.80 kHz | Streptothrix | 719.15 kHz | Streptococcus Pyrogen. |
233.00 kHz | Gonorrhea | 769.000 kHz | Tuberculosis (filterable) |
234.00 kHz | Tetanus | 769.035 kHz | Coli (filterable) |
369.43 kHz | Tuberculosis (rod) | 788.70 kHz | Syphilis |
416.51 kHz | Coli (rod) | 1.4452 MHz | Typhoid Fever (filterable) |
426. 86 kHz | Spinal Meningitis | 1.52952 MHz | Cancer Sarcoma (BY) |
477.66 kHz | Staphylococcus Aureus | 1.60745 MHz | Cancer Sarcoma (BX) |
Table 1. The Rife-Hoyland list of resonance frequencies for different pathologies.
frequency for BX is 1607.45 kHz. It was thus produced by choosing f = 21.275 kHz, while n = -4 and n' = 2. This procedure is quite complicated, but similar to normal practice for broadcasting. It did also protect Rife’s invention, without requiring patenting, since it was not easy to find the adequate value of f.
When Hoyland passed away, Verne Thomson became Rife’s new engineer. He built several ray machines and verified that the fine trimmed resonance frequencies of Table 1 are correct. We see there that the resonance frequencies are different, but unique for any particular type of microbes. Rife attributed this fact to their “chemical constitution” (p. 20 of the report). It was not yet possible to be more explicit, but the empirical result was already very important.
Today, it is possible to use frequency generators and hand-held electrodes. We were surprised when we examined a system, promoted in a book (Frequenz Therapie, German Edition, 2014). It contains an enormous list of resonance frequencies, without explaining how they were determined. It states for instance that they are 21,275 Hz for the BX carcinoma and 20,080 Hz for the BY sarcoma. These values differ from those of Table 1. Moreover, the book preconizes for instance 11 frequencies against “lack of appetite”. They are very low, since even 10 of them are situated between 20 and 1865 Hz, while 63 frequencies were listed to treat hepatitis C. This contradicts Rife’s result: there is only one resonance frequency for every type of microbes. Another list of frequencies, claimed to be Rife frequencies [48] provides also many relatively low frequencies, without any detailed justification. Only 4 of the 11 frequencies of the previous list are given here for lack of appetite, but 52 frequencies are provided for cancer. They range between 120 Hz and 795.6 kHz. It is prudently stated that these frequencies are “only for experiments”, but “you can see if they work for you”. Anyway, the apparatus is sold with much publicity.
We are afraid, of course, that this kind of business can constitute a serious obstacle to scientific recognition of Rife’s method and have to conclude that objective control and authorizations are needed, as for most professions and technical equipment. The biomedical engineer Marcello Allegretti reviewed medical applications of EM waves in several books, to make them understandable in general terms [49]. However, we never found an explanation of targeted destruction of microbes by resonance. It has to be possible for any real phenomenon.
Our first task was therefore to verify if there are visual proofs of the efficiency of Rife’s method. In addition to the trustable test for curing cancer patients, Rife made numerous microphotographs and movies to document his observations [50], but nearly all of them were stolen or destroyed. Nevertheless, some proofs were saved. We recommend two easily available videos [51] to see with our own eyes what happens. The video “Royal Rife-in his own words” shows instruments, procedures and (at minute 6:58) the turquoise-blue nanobacteria that he discovered. “The Royal Rife story” shows several times bursting bacteria (6:45, 6:59, 7:12, 8:37 and 9:07). Other videos [52] provide more background information.
John Crane presents in “Dr. Royal Rife’s 1939 lab film”the working place and equipment, used by Rife. The first pictures of the BX (14:33) were taken with Rife’s microscope of 1922. Bacteria are much larger and could already be observed with standard optical microscopes, even when they exploded (34:25, 34:45 and 35:15). The longer version of “Rife in his own words” displays turquoise-blue nanobacteria (7:39) and green ones (8:53). Drawings of the BX and the BY entities (15:23, 16:23) indicate the presence of pili on their surface. Nanobacteria can even be seen together with the corresponding bacteria (41:12). “The Rife story” includes more images of exploding bacteria (15:48, 16:02, 16:15, 1.56:03 and 1.56:14).
4. Explanation of Microbe Destruction by Resonance
4.1. Formulation of the Basic Problem
The first method that is customarily used when we are faced with unexplained phenomena is to make them plausible by referring to analogies. In a video of outstanding pedagogical quality, the music professor Anthony Holland used this method, since it is possible to shatter a wine glass by sound waves of adequate frequency [53]. The resonance frequency can be determined by tapping the wine glass or by rubbing its rim with a moist finger. The resulting stick-slip friction yields a continuous sound as for the bow and a vibrating string of violins. Though there are several modes of vibration for wine-glasses and bells, the dominant one corresponds to deformations of the rim along two orthogonal axes, as indicated in Figure 9(a). When the intensity of the exciting sound wave is strong enough, the glass is shattered, since it is quite brittle.
The relevant concept can be visualized in a more transparent way by means of a loop of steel wire, attached to a vertical vibrator that is activated by a frequency generator. There appear then “standing waves” with 4 knots for the lowest resonance frequency. More knots than in Figure 9(a) are also possible at higher frequencies. Figure 9(b) represents a “singing bowl”. This is a very old musical instrument, still used in China, Tibet and other Asian countries. It was made of bronze and vibrates like a wineglass, but does not break. When it is partly filled with water, bouncing droplets appear for strong enough excitation [54]. Nevertheless, these systems provide merely examples of normal resonance phenomena. Small scale surface waves of water result from surface tension and it is well-known that cohesion can then lead to the formation of drops.
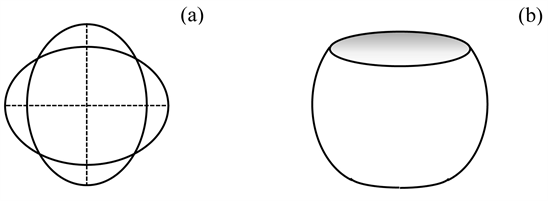
Figure 9. (a) Deformations of a vibrating wine glass. (b) A singing bowl or standing bell.
The spectacular collapse of the Tacoma Bridge is often cited as an example of resonance phenomena, but this resonance concerned a twisting vibration of the bridge that caused turbulent wind. This turbulence amplified the vibration and vice-versa, as visually explained in a video [55]. Positive feed-back can thus lead to auto-amplification and stronger resonances than normal ones. We will show that targeted destruction of viruses and other microbes results from such a mechanism and does also end with fatal disruption.
Anthony Holland did perform himself experiments concerning the effects of EM waves. He showed the results for a harmless unicellular organism, called “blepharisma”. Its usual size is 75 - 300 μm and can thus easily be observed with a standard optical microscope. These entities are elongated and their surface is uniformly covered with short hair-like organelles (see Wikipedia). Holland’s video [53] shows (at minute 10:43) that the membrane displays a blister before breaking up (11:13). It is interesting that another blister was forming at the other side (11:03) and that a small apparently exploring entity was unaffected at the imposed frequency. Holland showed then also exploding leukemia cells (13:00-13:24), by using the phanotron of a “Bare/Rife device”.
James Bare is an MD, wanting to help patients. It is respectable that he tried to understand what happens, but it is instructive to examine his attempted explanations to become aware of possible pitfalls. The term “resonant light technology” is not adequate, since the resonance is due to an EM wave and not by the luminous electron beam. Dr. Bare knew that, but he thought that it constitutes a “small antenna”. He mentions even “solitons” [56], but an antenna is only a conducting wire, where electrons are set in longitudinal oscillation to produce a standing wave with maximal amplitude at both ends. This is the usual way to create EM waves, but we explained already that Rife produced EM waves by deceleration of electrons in the anode.
Since the microscope revealed that the membrane of nearly spherical cells was locally broken up, Dr. Bare and collaborators thought that the resonance is due to the hole. A spherical vessel with a short neck constitutes a “Helmholtz resonator”, since the air in any closed vessel acts like a spring on the oscillating air in the neck. The resonance does spontaneously appear when an airstream is blowing fast enough over the opening, since stationary waves are then excited by turbulence, as inside some flutes. However, there is only one resonance frequency for a given size of the vessel and its neck, since there is a single oscillator. For flutes, there are several possible standing waves of different frequencies. Actually, the hole in the membrane of an exploding cell is a consequence of Rife’s resonances and not its cause.
To explain the destruction of viruses and microbes by resonance, it is necessary to start with adopting an adequate model. Holland’s analogy with shattering a wine glass could suggest that Rife excited deformations of the cell body. This would yield an ensemble of resonance frequencies [57], while Table 1 attributes only one resonance frequency to any particular type of microbes. Another possible hypothesis would be an electric polarization of the cell body. This mechanism leads to a resonance for particles that are very small compared to the wavelength λ of EM waves. They are bathing in a homogeneous electric field that induces surface charges, creating a secondary electric field inside the particle. It leads to a resonance for dipole oscillations. This accounts for the blue sky, since the electric field of sunlight does polarize very small particles in atmospheric air. This resonance frequency is situated in the domain of UV light and energy is only absorbed at this resonance frequency, but scattered at neighboring frequencies. This so-called “Rayleigh scattering” of sunlight results from the induced polarization. It is more intense for blue than for red light. This theory applies also to collective oscillations of electrons in very small metal particles and allowed us to explain the “anomalous optical absorption” of thin granular metal films [58]. The same theory explains the resonance that radio-waves produce in red blood cells [59]. However, the mechanism of Rife’s resonance phenomenon is different and has not yet been explained.
4.2. Structure and Function of Virus Spikes
The Covid-19 pandemic and images of the relevant viruses suggested to the author that their spikes might be set in oscillation and could perhaps lead to a devastating resonance. We will test this hypothesis by establishing the relevant equation and solving it, but first of all, we had to know more about the structure and function of virus spikes. They are not merely flower-like decorations, but very efficient weapons for attacking cells, in order to use their machinery to reproduce themselves in great numbers.
The so-called “Spanish flue” of 1918 was due to a virus. It infected some 500 million people and killed at least 20 million persons [60]. This virus became more lethal during the pandemic, since its mutation led to a second wave, where lungs were filled with blood. The Corina-19 virus appeared in China and was partially controlled by containment, but not stopped. Social proximity, increased population densities, worldwide mobility and interwoven economies are major factors of its spreading. We see also that the search and testing of vaccines take time. Even a vaccine cannot protect us against unpredictable new mutations and the possible appearance of more virulent forms. It would thus be irresponsible to neglect already existing evidence that an efficient,safe and rapidly adaptable biophysical method is possible.
Rife’s method could have been tested at least by means of experimental procedures, but it was rejected since it seemed to be unbelievable. Nevertheless, it is also necessary to explain why the reported facts are true. We are thus confronted with a basic scientific problem. There are numerous examples, indeed, where something unexpected was discovered. It concerned still hidden realities. How can we get access to anything that is not directly observable? We have to imagine what might happen, draw logical consequences from this hypothesis and verify then if they are true or not. The first problem is thus to select a plausible hypothesis, deserving rigorous analysis ...
It became possible at about 1980 to combine cryogenic electron microscopy with gene sequencing to understand the role of spikes. The resulting knowledge is summarized in Figure 10, but for clarity, we represent only one pair of macromolecules, while the flower-like hemagglutinin (HA) spikes contain 3 identical pairs. We are now accustomed to artistic representations, but they do not reveal what is essential. Figure 10(a) represents the normal state of the associated HA1 and AH2 proteins. The HA1 molecule contains negative charges (COO–) that belong to small sialic acid molecules that can move inside the molecule. Because of their mutual repulsion, they create surface charges. Electrostatics tells us that its density depends on the configuration of the surface and has to be greater near the pointed tip of the HA1 molecule.
These charges polarize the electrically neutral HA2 molecule, which is a slender, helicoidally wound molecule. It tends to be straight, but is bent and kept in this state, because of the increased surface charges at the lower end of the HA1 molecule. The middle part of the coil spring is more irregular than indicated here, but it is only important that we get a loaded spring trap. It is anchored in the membrane of the virus. Tts extremity, represented in green in Figure 10(a), is situated on the other side of the membrane of the virus. It is electrically charged and thus hydrophilic. This is usually sufficient to secure the implantation, but not for very strong traction.
Figure 10(b) shows what happens in the vicinity of a cell. Its pores allow ion transport that maintains a potential difference between the inner and outer surface of its membrane. This leads to an increased density of H+ ions near the external surface. When a virus comes close to the membrane, these protons reduce the surface charge density of the HA1 molecule, since COO– + H+ → COOH. The remaining surface charge is then too small to keep the HA2 spring in its bent state. It is suddenly released and its tip carries a fusion protein, indicated in red. It penetrates the membrane and this occurs simultaneously for the three HA

Figure 10. Schematic representation of one pair of HA1 and AH2 molecules, constituting spikes of viruses. (a) In the normal state, the helically wound molecule HA2 is bent and kept in place like a loaded spring. (b) It is released by neutralization of the HA1 molecule.
pairs. The redundancy strengthens the grabbing, as well as the rooting. Moreover, the structure of the HA1 part is modifiable by mutations to prevent the immune system from recognizing the potential invader. Viruses are terrorists, carrying jackknifes under a coat. They are ready for stabbing cells that are in reach and their camouflage can be modified to escape detection. The HA2 part is on the contrary strictly conserved. This ingenious system was elaborated by natural selection, governed by survival of the fittest.
The existence of this war machine was recognized in 1993 [61]. To highlight the rapidly expanding research on this subject, we mention the review of the virologist Suzuki and a molecular biochemist [62]. Professor Stephen Harrison of Harvard medical school presented this theory in an excellent video [63] and explained how the spikes help the virus to penetrate into the cell [64]. We insist more on explaining the mechanism of automatic triggering. It is known that spikes of the SARS-2 virus have a conical form [65]. It differs from usual representations, although it is also attached to the membrane by a thin stalk.
4.3. Other Spikes of Viruses and the Pili of Bacteria
So far, we described only virus spikes that are made of hemagglutinin (HA), but viruses do also have another type of spikes. They are constituted of 4 neuraminidase (NA) proteins, which are also electrically charged [66]. 18 variants of HA and 11 subtypes of NA are known [67]. The phylogenic tree of the Corona virus [68] indicates thus quite great variability. Viruses were modified to become more efficient. The influenza virion carries 300 to 400 HA spikes and 40 to 50 NA spikes. Their relative numbers have to be balanced [69], since they cooperate to help the virus to get inside the pirated cell. The diameter of the spherical core of usual viruses is about 120 nm. The length of HA spikes can be about 12.5 nm long, while the length of NA spikes is slightly smaller or greater.
Rotaviruses are different. They contain double-stranded RNA, instead of single-stranded one and are said to be non-enveloped. Actually, the lipid bilayer is replaced by a tightly fitting protein coat, but there are always spikes that undergo conformational changes and perforate the lipid bilayer of the target cell [70]. Bacteria are endowed with long corkscrew-like flagella. They allow for efficient propulsion, since they are activated by small individual motors, embedded in the cell membrane, but the whole surface of bacteria is covered with pili. The growth and molecular constitution of these hair-like structures are now well-known. The major part is a helical fiber with a sticky tip. This allows for adhesion and some stretching that causes retracting forces. The rod is hollow and can even allow for DNA transfer, but is also an electron conductor. The main function of pili or cilia of bacteria is to sense their environment and to facilitate sexual reproduction by fusion with the same type of bacteria. Antibacterial molecules interfere with this process, but do not prevent survivors from producing protective mutations. For us, it is essential that pili do also carry positive and negative parts [71], since that offers the possibility to act on them by means of an oscillating electric field.
4.4. The Normal Resonance and Parametric Amplifiers
To facilitate a rational understanding of Rife’s resonance, we begin with analyzing the properties of a simple and familiar system. A pendulum is merely composed of a mass M, suspended at a fixed point by means of a string of constant length L. Figure 11(a) shows that an angular displacement θ with respect to the vertical implies a horizontal displacement
Every dot indicates a derivation with respect to the time variable t. The solution of this equation is
If air friction were really negligible, the amplitude C would remain constant. Actually, the oscillation is progressively damped, since the mass M is subjected to air friction. This braking force is proportional to the instantaneous velocity
Figure 11. (a) Parameters needed to describe the motion of a simple pendulum. (b) The peak for possible amplitudes of forced oscillation is very high and narrow for low friction.
Thus,
The solution (7) describes forced oscillations that subsist when the initial conditions are not relevant anymore, because of damping. The mass M is oscillating at the imposed frequency ω, but the constants A and B are determined by substituting Equation (7) in Equation (6). We get then
Thus,
Because of (7),
These expressions describe the normal resonance phenomenon. Rife’s resonance is more powerful, but the first relation (8) is already very useful to understand the physical meaning of resonances. The amplitude C of forced oscillations is maximal when the denominator is minimal, this happens when its derivative with respect to ω is zero and thus when ω = ων, where
In general, the height of the peak is S/4ν2 and its width at half height is equal to ν. The resonance becomes thus sharper for decreasing friction. The amplitude C would even become infinite in the absence of friction. The second relation (8) predicts the phase difference φ for different values of ω. This function is represented in Figure 12(a) for ωo = 1 and ν = 0.02. The change of sign means that the oscillator is able to follow the rhythm of the applied force when the imposed frequency is lower than ωo, but it stays behind when it is too fast.
We are now ready to answer a simple question: is a child, sitting on a swing, able to sustain itself the oscillations without any external help? Probably, you found the answer yourself by trial and error. It is fun to make discoveries and to master a situation oneself. It is even much more interesting and surprising to understand why this is possible. The child has to straighten up when it is approaching the highest points and to incline backwards when it is moving towards the other side. The effective length L of the pendulum is thus modified as shown in Figure 12(b).
Figure 12. (a) The phase difference between the forced oscillation and the applied force. (b) This type of periodic variations of the effective length L of the pendulum yields a parametric amplifier.
The variation of L can be approximated by the function
The variation of the parameter L is adapted to the actual frequency of oscillation, but the equation of motion (6) is then modified. It yields
To solve this equation, we note that
This relation was proven in trigonometry, without mentioning its physical importance. The fact that the product of two oscillating functions is equivalent to a sum of two oscillating functions implies that Equation (9) is equivalent to
The periodic variation of the length L produces thus two oscillating driving forces. The first one does exactly compensate friction when ω = ωo and γ = 2ν/ωo. The other force has negligible effects, since the frequency 3ω is too far away from the resonance frequency. The child can thus sustain the oscillations by its own muscular forces. Greater values of γ will not only compensate energy losses, but increase the amplitude. The system becomes then a parametric amplifier until equilibrium is reached. This can easily be verified by attaching a small mass on a string that is partially wrapped around a pencil. It is sufficient to rotate the pencil towards the left and the right at the adequate rhythm. Trapeze artists apply this method at a human scale.
We transposed this theory to explain the mysterious phenomenon of ball lighting [72]. Since skeptics did simply attribute it to illusions, in spite of numerous testimonies of serious witnesses, it is useful to show how the explanation was found. The example is also adequate to illustrate the method of imagining what is hidden and verifying if the logical consequences do agree with all observed facts. We assumed that ball lightning is similar to a soap bubble, but that the membrane is luminous, since it contains ionized air. However, light emission results from recombination processes. The luminosity should decrease very rapidly, as for ordinary lightning. The difference is that the membrane allows for collective motions of the free electrons with respect to the heavier ions inside the membrane. The frequency ωo of this “plasma oscillation” is determined by the density of free electrons, but they are radially oscillating inside the membrane. This makes the external surface alternatively positive and negative. Ball lightning does thus alternatively attract electrons and positive ions that are present in the ambient air near its surface. This replenishes not only the stock of charged particles, but modulates also the oscillation frequency as in Equation (9). This leads to auto-oscillations. They are sustained without requiring constant excitation by an oscillating electric field of external origin.
How can we test the validity of this explanation? The answer is that it accounts for apparently mysterious observations. Indeed, ball lightning is usually moving around in an apparently erratic way. We can now “mentally see” that it is constantly attracted towards the greatest density of charged particles in the ambient medium. It behaves thus like a living being that survives by feeding itself. Moreover, ball lightning can suddenly disappear in midair, as if the light had been extinguished. This is due to entering a region where the ambient air was not sufficiently ionized. It can also happen that ball lightning explodes, even very violently. The invisible cause is a locally greater ionization of the ambient air, which led to fatal parametric amplification. Although this was a digression, it is useful to understand an essential feature of science and to be prepared for another intellectual adventure. It concerns the destruction of viruses and other microbes by means of resonances, but they are quite special.
4.5. The Peculiar Resonance of Virus Spikes
The analogy with shattering a wine glass [49] is useful as a first approximation. It begins also with determining the resonance frequency and an experienced singer is able to produce a sound wave of precisely the same frequency. With laboratory instrumentation, we can prove that there are several possible ones and select one of these frequencies to produce a resonance [73]. Spikes can also be set in forced oscillations, but the resulting resonance is more powerful than normal resonances. Figure 13(a) shows the outline of the spikes of the Corona virus, according to data obtained by means of cryo-electromicrography [74]. The spike is normally straight and we know that its upper part is negatively charged. Figure 13(b) reduces the spike to its essential elements. It is then similar to a cantilever that is implanted in a larger body, but can be bent, when its effective tip

Figure 13. (a) The global shape of a Corona virus spike in its normal state. (b) The applied force produces a lateral displacement and allows for a powerful resonance.
mass Mo is subjected to a lateral force F. It produces then a displacement x with respect to the symmetry axis. How does it vary for an oscillating force?
Fortunately, Friswell’s team established already in 2012 the equation of motion for energy harvesters [75]. They consist of a homogenous elastic beam that carries a tip mass and is implanted on a chariot. It is set in motion by random oscillations of a bridge and the resulting kinetic energy is transformed by detectors into electric energy. We adapt their equation to describe possible vibrations of virus spikes. The difference is only that their base remains fixed, while the oscillating force F is directly applied to the tip mass Mo. Although the stem of the spike is not homogeneous, we can keep the model of a uniform beam by defining average values. However, the spike is surrounded by a fluid instead of air and thus subjected to viscous friction. The equation of motion is then
where
The effective mass Mo is thus defined by the real tip mass M, the length L of the beam and its averaged mass density μ. It is also necessary to account for the moment of inertia I of the spike with respect to the fixed point. The stiffness of the beam is mainly determined by the coefficient k, which depends on Young’s modulus E of the constituting material, the length L of the cantilever and its moment of inertia I. For energy harvesters with a very flexible beam, the weights of the tip mass M of the beam will reduce the restoring force. This allows for two lateral equilibrium positions along a given direction. The nonlinear terms of Equation (11) lead then to chaotic behavior. where the tip mass can execute small oscillations around one of the possible equilibrium positions, but also pass from one side to the other. Indeed, very small changes of the instantaneous position and velocity at critical moments will produce qualitatively different motions. For spikes, surrounded by a fluid, we can neglect the weights because of buoyancy, but the nonlinear effects remain important. Actually, the equation of motion (11) is reduced to
The spike does not simply behave like an inverted pendulum, since Equation (6) is generalized. The nonlinear terms depend on the instantaneous values of the displacement x, the velocity
The value of φ depends on ν, but when
The nonlinear terms in Equation (12) are again equivalent to adding two forces. They oscillate at the frequencies ω and 3ω. The first one modifies the applied force and the second force can be neglected, since the frequency 3ω is too far off-resonance. To concentrate on essential features for the resonance, we assume that friction is negligible (ν = 0 and φ = 0). The amplitude C of forced oscillations is then determined by Equation (12), which yields
Indeed,
Thus
without nonlinear effects, we get the normal resonance. It corresponds to (8), but is simpler, since ν = 0. It is represented by the black graph in Figure 14(a) and represents the actual amplitude of forced oscillations with a change of sign below and above the resonance frequency. It differs from Figure 11(b), which accounted only for the magnitude of C(ω) when ν = 0.02, while the sign was determined by Figure 12(a). Nonlinear effects do modify the response of spikes, since Equation (13) allows for 3 possible solutions and in particular for
Figure 14. (a) The amplitude of forced oscillations of spikes would be Co(ω) without nonlinear effects. The resonance frequency is then ωo = 1. Nonlinear effects allow for auto-oscillations, characterized by C1(ω). (b). This leads to a synergy when it is combined with constant excitation and yields then C(ω).
We expected, of course, that without excitation there is no response, but because of nonlinear effects, spikes are able to produce a driving force that yields auto-oscillations. This is similar to what happened for a pendulum, when its effective length was periodically modified, but the reason is different. Now, it does not compensate friction, since we considered even the case where ν = 0. The stiffness of spikes allows them to oscillate by themselves, but only in a limited frequency domain, since C2 has to be positive to yield a real value for the amplitude C. It is necessary that
The rigorous treatment of this problem was necessary, because of past contestations. It is also instructing from a theoretical point of view, since it illustrates the usually hidden mechanism of nonlinear systems. Moreover it is and should be of great practical importance. We can now harvest the fruits. We measured displacements in units L = 1, but when the mass M is dominant, the moment of inertia I is proportional to L2. The value of
4.6. The Mechanism of Targeted Microbe Destruction
Constructing a theory consists in choosing a plausible hypothesis and deducing logical consequences. Even a correct theory is only valid when its predictions agree with all known facts and further experimental verifications. Figure 15(a) represents a cantilever that is set in forced oscillation at a frequency ω that is close to the resonance frequency. When ω = ω1, the amplitude C of the oscillation
Figure 15. (a) Forced oscillations of a spike or pili. (b) At resonance, it is extracted and creates a hole in the membrane that destroys the microbe by extrusion of its content.
becomes quasi infinite, even when friction is not totally negligible. Resonance would thus imply enormous stretching of spikes or pili, if they were solidly implanted in the membrane or any equivalent structure. Normally, this would cause plastic deformations and eventually fracture, but that is replaced by extraction from the membrane and creation of a hole.
This causes expulsion of the content of the virus, as represented in Figure 15(b). The virus is definitively destroyed. We recall that spikes are only fastened by the hydrophilic tail of their backbone, represented in green. This fixation is usually sufficient, but not secured, as can be achieved by means of bolts and screws. This system was invented in Antiquity at about 400 BC and it was recognized that the screw has to be well-tightened. The explanation is that dry friction between nonmoving surfaces is greater than kinetic friction and increased by pressure. This insight came much later and required even repeated discoveries [by da Vinci, Amontons and Coulomb, respectively at about 1500, 1700 and in 1785]. The fastening of spikes is improved by triple implanting, but not enough to resist at the resonance frequency. Even trees can be deracinated by strong wind, in spite of their distributed roots.
This theory applies also to pili, covering the surface of bacteria and nanobacteria. Since they carry electrical charges, they can also be set in forced vibrations by an oscillating electric field. They behave like cantilevers that can be elastically bent, but because of nonlinear effects, they allow for auto-oscillation and extremely great amplitudes of oscillation at their resonance frequency ω1. The creation of a hole and destruction of microbes could be observed. Holland’s video [53] shows even local bulging of the membrane of bacteria before the explosive eruption. This means that a bunch of pili was involved at a place, where the electric field was perpendicular to these structures. Bulging began also at the opposite side, where the electric field is also effective. Moreover, microbes are immobilized before breaking up, since the propelling function of pili is already disturbed. It does not only depend on motorized flagella.
The sophisticated spikes of viruses are highly efficient weapons, but they have an inherent weakness that can be exploited when we are aware of this possibility. Although pili of bacteria and nanobacteria have other functions, they lead also to total destruction, without survivors that could initiate securing mutations. It is only necessary to impose a frequency that is precisely equal to the resonance frequency. It was a huge error to claim that the observed facts had to be bogus, even without verifying, since it deprived humanity from making use of a simple and secure method to fight sicknesses, plagues and even cancer.
Rife found not only that BX and BY bacteria are involved in cancer, but also that they are proliferating after radiotherapy. This merits special attention. It has been rediscovered that oscillating electric fields can be used for cancer therapy. A possible mechanism has been proposed [76] [77], but it is still a hypothetical one and should be reexamined in a larger context. Since pleomorphic transformations are reversible, it is plausible that the total number of pili is conserved in size reduction. Their surface density would then be increased for nanobacteria and explain why they become more virulent. Nevertheless, they remain vulnerable for Rife’s resonances.
It should be noted that a cantilever, constituted of a steel wire, does also allow for another mode of oscillation, where a knot is created near the free end. However, the resonance frequency is significantly higher and this type of deformations can be excluded for virus spikes. We mention also that it is possible to use UV light for disinfecting surfaces. Low pressure mercury lamps produce UVC light at 254 nm. It is absorbed by RNA and produces there local defects [78], but this method is only applicable to viruses that are directly exposed to this radiation on a surface, in aerosol droplets or very thin liquid films. The FDA issued a warning, since UVC light damages the human skin and is dangerous for our eyes [79]. Rife’s method is not dangerous at all and efficient for destroying virulent microbes anywhere inside our body.
Rife did prove that optical microscopes allow for much greater magnification and higher resolution than had been assumed. Since he constructed himself several supermicroscopes with purely classical means, his scientific creativity and accomplished craftsmanship deserve recognition and respect. With his instruments, he could clearly observe that when bacteria are exposed to stress, they reduce their size. They keep only what is essential to survive, but are more aggressive. Naessens did also prove the reality of pleomorphism, but some authorities did not like that. They declared that these pioneers are quacks, but refused to verify if the reported facts were real or not. This attitude is more than strange.
Moreover, Rife discovered already about 100 years ago that bacteria and nanobacteria can be destroyed by resonance. His phanotron was an ingenious instrument that produced the required electric field by means of braking radiation. Instead of emitting EM waves in all directions by means of an antenna, like Hertz did and is usual for broadcasting, his system generated a local beam of EM waves. The destruction of bacteria by resonance was already observable with standard optical microscopes, but Rife was also able to see exploding nanobacteria. Actually, he had to persevere during more than a decade to make these tiny microbes visible. He did then prove that some of them are present in cancer tissue and that after being cultured, they do also cause cancer. He determined the resonance frequency for targeted destruction of various microbes. These values were confirmed by two collaborators, using different equipment.
The efficiency of his method for healing cancer was clinically tested, but even these results were declared to be bogus, since they required modifying cherished postulates. For those who had the power to crush Rife, it did not matter that the reported results might be true. Rife was prosecuted. His documents were stolen. Instruments were wrecked and all traces of his achievements were eradicated from official medical records. That was profoundly unjust,truly antiscientific and detrimental for the worldwide health system.
We solved the basic scientific puzzle with mathematical rigor by considering that spikes of viruses, as well as pili of bacteria and nanobacteria can be set in forced oscillation. Nonlinear effects make the resonance stronger and sharper than usual ones. There is only one resonance frequency for every particular type of microbes. It depends on the length of the oscillating structures and is thus specific. This theory is experimentally confirmed and leaves no rational reason to negate the possibility of targeted destruction of microbes. The author of this study has no financial interest whatsoever in a general implementation of this method. His concern is merely truth, justice, but also reduction of unnecessary suffering and death. Other persons and institutions have now to go on in the direction that was pointed out by Rife.
The Coronavirus pandemic and its social implications should make everyone attentive to the existence of a biophysical method that differs from the usual biochemical one, but is effective,secure and rapidly adaptable. It is only necessary to determine the adequate resonance frequency very carefully, but this can be done with inexpensive equipment and by means of direct microscopic observation. Even the constant threat of unpredictable mutations can rapidly be countered. The treatment of patients requires only a few minutes, at intervals of three days. Because of the sharp resonance, this method is selective and can eliminate side effects when it is objectively controlled like cars and traffic, for instance.
There is also rising evidence that our precious arsenal of antibiotics is endangered. Multiple antibacterial resistances are increasing [80]. The US Centers for Disease Control and Prevention concluded already in 2015 that “coordinated efforts to implement new politics, renew research efforts, and pursue steps to manage the crisis are greatly needed.” This was thought to “require considerable investment of human and financial resources”, but that is not true for Rife’s method. Basically, it only required to change some habits of though.
We have to insist that dogmatism and concentration of power endanger scientific progress by blocking freedom of thought. When it is guided by observing reality and rational analysis, it is more efficient than ideology,but dictatorship and reckless use of power are always a temptation. In this context, we have to mention the research of the Russian chemist Tamara Lebedeva [81]. She made intensive research on trichomonade parasites and proved that they can cause cancer. Their reproduction rate was found to be increased by radiotherapy, but Lebedeva’s work was not recognized by medical authorities. Alfons Weber studied the impact on cancer of protozoa causing malaria [82]. He published his results in 1967 and promptly lost his approbation as medical doctor. It is now appearing that there are connections between malaria and cancer [83]. The plasmodium parasite is involved in both fields and cross-fertilization in medicine should be encouraged. The common feature of the research of Lebedeva and Dr. Weber was to consider that cancer is an infectious disease. We have to add that these types of parasites are not the only possible cause of cancer, but their effects should also be investigated.
To provide a concrete and still actual example of tenacious preconceptions related to medicine, we mention that Dr. Jacques Benveniste did experimentally prove the existence of “water memory” in the 1980th. Nevertheless, it was declared (even by a world-famous scientific journal) that this is impossible. This claim was based on the apparently obvious idea that when biologically active molecules are repeatedly dissolved in water, they cannot be active any more when all of them have been eliminated. Since Benveniste found that the final solution did produce the same effect as if these molecules were still present, this fact required an explanation. From a scientific and human point of view, it is shocking that it was accepted to pretend that Dr. Benveniste and his team were merely victims of an illusion. The real problem required to verify if the active molecules could be replaced by substitutes, resulting from structuring water. Is it really impossible that thermal agitation of water molecules in the liquid state could cause structuring of water molecules according to the initial template?
Since this concerns condensed matter physics, we tried to solve this problem and published in 2018 a rational explanation [84]. Since water molecules are dipolar, they can constitute very dense crystallites, where all these dipoles have the same orientation. We proved that they are spherical and so small that they could not be observed with standard optical microscopes. These nano-pearls are formed by the electric field of charged parts of biologically active molecules. Being also dipolar, these “water pearls” constitute chains, where they are set in rotation at the frequency of the vibrating charged part of active molecules. The resulting standing wave limits the length of these chains by preventing further growth. Since the length of these chains depends on the frequency of oscillation of the charged part of active molecules, they become relevant information carriers. Their existence is real.
They are even multiplied by successive dilutions, always accompanied by vigorous shaking, since some chains are then broken, but are reconstituted by the oscillating electric field of the majority of intact chains. This process yields numerous efficient substitutes of the active molecules. It explains also about a dozen other experimental observations, made in the meantime. It accounts even for homeopathy, which is at present under harsh attack by those who claim that these products can merely act as placebos. Without understanding the real mechanism, it is more difficult to abandon preconceptions, but it is surprising that even a high-level “Scientific Advisory Council” did participate in lobbying to eliminate homeopathy by legal procedures [85]. Ideology and financial interests can even overrule normal scientific procedures.
This fact has to be combined with objective evidence that pharmaceutical industries are radically and recklessly oriented towards big profits in a capitalistic way. This dreadful situation was recently documented by Luc Hartmann [86] and shows that Big Pharma is out of control. This is not always true, of course, but according to trustable authorities [86], they can indirectly pay institutions that should evaluate the efficiency, as well as already reported side effects. Political and legislating authorities should urgently react to avoid more scandals and flagrant injustices.
Rife made a great discovery. We did only explain why apparently unbelievable, but observed facts are true. Now it is up to other persons and institutions to carry on. The fast development of vaccines merits praise, but there is now much more at stake than protection of already gigantic industrial empires. We appeal therefore to the World Health Organization, all Ministers of Health and Governments, as well as the United Nations to initiate and organize also another way to cope with unnecessary suffering and death. That is possible and urgently needed.
The author wants to thank Dr. Med. Jens Wurster for informing him about Rifle’s work and many interesting exchanges of ideas, as well as a careful, unknown referee for constructive remarks.
Conflicts of Interest
The author declares no conflicts of interest regarding the publication of this paper.
| [1] | Lynes, B. (1987) The Cancer Cure That Worked! Fifty Years of Suppression. BioMed Publishing Group, South Lake Tahoe. |
| [2] | Masters, B.R. (2010) The Development of Fluorescence Microscopy. Wiley Online Library. https://doi.org/10.1002/9780470015902.a0022093 |
| [3] | Anonymous (2017) Royal Rife’s Universal Microscope (and Why It Can’t Exist). Blog. http://sustainable-nano.com/2017/08/18/royal-rifes-universal- microscope-and-why-it-cant-exist |
| [4] | Wade, G. (2014) The First Rife Microscope and the Gained Ability to Observe Viruses and the Fine Structure of Bacteria with an Optical Microscope. https://www.rife.de/observe-viruses-and-bacteria.html |
| [5] | Kungliga Vetenskapsakademien (2014) The Nobel Prize in Chemistry 2014. Scientific Background. https://www.nobelprize.org/prizes/chemistry/2014/advanced-information |
| [6] | Seidel, R.E. and Winter, M.E. (1944) Journal of the Franklin Institute, 237, 103-130. http://www.pulsedtechresearch.com/wp- content/uploads/2013/04/New-Microscopes-SeidelWinter.pdf https://doi.org/10.1016/S0016-0032(44)90203-6 |
| [7] | BRMI (2018) History—Dr. Royal Raymond Rife Jr. https://www.brmi.online/royal-raymond-rife |
| [8] | Comparet, B.L. (1960) Questions and Answers. Rife Research Europe: An Interview with Rife. https://www.rife.de/an-interview-with-rife.html |
| [9] | Neuman, R.O. and Mayer, M. (1914) Atlas und Lehrbuch wichtiger tierischer Parasiten und ihrer überträger. https://jamanetwork.com/journals/jama/fullarticle/438846 |
| [10] | Kendall, A.K. and Rife, R.R. (1931) California and Western Medicine, 35, 409-411. https://europepmc.org/article/med/18741967 |
| [11] | San Diego Union (1929) Local Man Bares Wonders of Germ Life. New Apparatuses Unveil Hidden Microbe Universe to Human Eye. https://rifevideos.com/local_man_bares_wonders_of_germ_life.html |
| [12] | Rife, R.R. (1953) History of the Development of a Successful Treatment for Cancer and Other Virus, Bacteria and Fungi. Research Lab. Data, San Diego. https://www.rife.de/files/history_rife_cancer_treatment.pdf |
| [13] | Rosenow, E.C. (1932) Science, 76, 192-193. https://www.rife.de/observations-with-the-rife-microscope.html https://doi.org/10.1126/science.76.1965.192 |
| [14] | Hess, D.J. (1996) Medical Anthropology Quarterly, 10, 657-674. https://doi.org/10.1525/maq.1996.10.4.02a00140 |
| [15] | Rife, R.R. and Crane, J. (1950) The Universal Microscope. RifeVideos.com. https://www.rifevideos.com/dr_rife_talks_with_john_crane_about_his_universal_microscope.html |
| [16] | Hell, S.W. (2014) Nobel Lecture. https://www.youtube.com/watch?v=9BzGB1SUPGQ https://www.nobelprize.org/uploads/2018/06/hell-lecture.pdf |
| [17] | Vangindertael, J., et al. (2018) Methods and Applications in Fluorescence, 6, Article ID: 022003. https://doi.org/10.1088/2050-6120/aaae0c https://www.chem.kuleuven.be/pd/static/publications/Vangindertael2018.pdf |
| [18] | Bonhams (2009) An Exceptionally Rare Rife Microscope. https://www.bonhams.com/auctions/16871/lot/113 |
| [19] | Elswick, S.R. (1994) The Amazing Wonders of Gaston Naessens. Super Microscopes and Suppressed Cancer Treatments. Nexus Magazine. http://www.whale.to/v/naessens.html |
| [20] | Naessens, G. (2010) The Somatoscope. https://www.youtube.com/watch?v=KGJW94ciq4c |
| [21] | Claxton, N.S., et al. (2006) Microscopy, Confocal. Wiley, Hoboken. https://en.wikipedia.org/wiki/Confocal_microscopy https://doi.org/10.1002/0471732877.emd291 |
| [22] | Bird, C. (1991) The Persecution and Trial of Gaston Naessens. Tiburon-Kramer. 336 p. |
| [23] | BRMI. History-Antoine Béchamp. https://www.biologicalmedicineinstitute.com/antoine-bechamp |
| [24] | Perrot, A. and Schwarz, M. (2014) Pasteur et Koch, un duel de géants dans le monde des microbes. Odile Jacobs. https://www.youtube.com/watch?v=YuC3T3eesDU |
| [25] | Henri, V. (1914) Comptes rendus de l’Académie des Sciences, 159, 340-343, 413-415. https://pubs.rsc.org/en/content/articlelanding/1914/ca/ca9140601112/Abstract#!divAbstract |
| [26] | Almquist, E. (1922) The Journal of Infectious Diseases, 31, 483-493. https://doi.org/10.1093/infdis/31.5.483 |
| [27] | Naessens, G. (2010) The Somatid and Its 16 Stage Cycle. https://www.youtube.com/watch?v=ttl5NBo3_Z4 |
| [28] | Klieneberger-Nobel, E. (1951) Microbiology and Molecular Biology Reviews, 15, 77-103. https://mmbr.asm.org/content/mmbr/15/2/77.full.pdf https://doi.org/10.1128/MMBR.15.2.77-103.1951 |
| [29] | Kurath, G. and Morita, R.Y. (1983) Applied and Environmental Microbiology, 45, 1206-1211. https://doi.org/10.1128/AEM.45.4.1206-1211.1983 |
| [30] | Folk, R.L. (1994) Interaction between Bacteria, Nannobacteria and Mineral Precipitation in Hot Springs of Central Italy. https://www.erudit.org/en/journals/gpq/1994-v48-n3-gpq1907/033005ar.pdf |
| [31] | Kajander, E.O. and Ciftcioglu, N. (1998) Proceedings of the National Academy of Sciences of the United States of America, 95, 874-879. https://doi.org/10.1073/pnas.95.14.8274 |
| [32] | Ciftcioglu, N., et al. (2006) Journal of Investigative Medicine, 54, 385-394. https://doi.org/10.2310/6650.2006.06018 |
| [33] | Cantwell, A. (1990, 1995) The Cancer Microbe. The Hidden Killer in Cancer, Aids and Other Immune Diseases. Aries Rising Press, Los Angeles, 281 p. |
| [34] | Cantwell, A. (2005) For Women against Cancer. Aries Rising Press, Los Angeles, 281 p. |
| [35] | Wainwright, M. (1997) Perspectives in Biology and Medicine, 40, 407-414. https://doi.org/10.1353/pbm.1997.0038 |
| [36] | Kumar, C.A., et al. (2011) Oral Medicine and Radiology, 23, 354-359. https://doi.org/10.5005/jp-journals-10011-1168 |
| [37] | Schlieper, G., et al. (2011) Nephrology Dialysis Transplantation, 26, 3436-3439. https://doi.org/10.1093/ndt/gfr521 |
| [38] | Ciftcioglu, N. and McKay, D. (2010) Pediatric Research, 67, 490-499. https://doi.org/10.1203/PDR.0b013e3181d476ce |
| [39] | Cantwell, A. (2014). https://livebloodonline.com/breast-cancer-caused-pleomorphic-bacteria |
| [40] | Duda, V.I., et al. (2012) Microbiology, 81, 379-390. https://doi.org/10.1134/S0026261712040054 |
| [41] | Luef, B., et al. (2015) Nature Communications, 6, 6373. https://www.nature.com/articles/ncomms7372 https://doi.org/10.1038/ncomms7372 |
| [42] | Krotz, D. (2015) First Detailed Microscopy Evidence of Bacteria at the Lower Size Limit of Life. https://newscenter.lbl.gov/2015/02/27/ultra-small-bacteria |
| [43] | Mattman, L.H. (1974) Cell Wall Deficient Forms: Stealth Pathogens. CRC Press, Boca Raton, 448 p. https://doi.org/10.1201/b16928 |
| [44] | Ramijan, K., et al. (2019) Nature Communications, 9, Article No. 5164. https://www.nature.com/articles/s41467-018-07560-9.pdf |
| [45] | Claessen, D. and Errington, J. (2019) Trends in Microbiology, 5, 1025-1033. https://www.cell.com/trends/microbiology/pdf/S0966-842X(19)30192-1.pdf https://doi.org/10.1016/j.tim.2019.07.008 |
| [46] | Vassilatos, G. (2003) Ultra Microscope and Cure Rays: R. Raymond Rife. Lost Science (See Spears). http://customers.hbci.com/~wenonah/history/rife.htm |
| [47] | Crane, J., March, J., et al. (2012) The Rife Machine Report: A History of Rife’s Instruments and Frequencies. 149 p. http://www.royal-rife-machine.com/the_rife_machine_report.pdf |
| [48] | Spooky 2 (2018) Rife Frequency List. Compiled by Spooky2-mall .com, 2018. https://s6c2n9k7.stackpathcdn.com/download/spooky2rifefrequencylist.pdf |
| [49] | Allegretti, M. (2018) The Therapeutic Properties of EM Waves. 154 p. |
| [50] | Dunn, H.H. (1931) Movie. https://www.rife.de/movie-new-eye-of-microscope-in-war-of-germs.html |
| [51] | Videos: Rife in His Own Words. The Royal Rife Story. https://www.rife.de/rife-related-videos.html |
| [52] | Rifevideos.com: 1939 Royal Rife Laboratory Film (John Crane, 35:34); Royal Rif in His Own Words (51:15); The Royal Rife Story (2.11:22). |
| [53] | Holland, A. (2013) Shattering Cancer with Resonant Frequencies. TEDx Talks (17:08). https://www.youtube.com/watch?v=1w0_kazbb_U |
| [54] | Terwange, D. and Bush, J. (2011) Tibetan Singing Bowls. https://core.ac.uk/download/pdf/4434335.pdf |
| [55] | Practical Engineering (2018) Why the Tacoma Bridge Collapsed. YouTube (8:48). |
| [56] | Dubost, G., et al. (2008) Theoretical Low Frequency Acoustic Resonances of Various Rife-Bare Antennas. https://www.researchgate.net/publication/273886201 |
| [57] | Baladin, A.A. and Fonoberov, V.A. (2005) Journal of Biomedical Nanotechnology, 1, 90-95. https://doi.org/10.1166/jbn.2005.005 |
| [58] | Rouard, P. and Meessen, A. (1977) Progress in Optics, 50, 79-137. http://www.meessen.net/AMeessen/optical_properties_of_thin_metal_films.pdf https://doi.org/10.1016/S0079-6638(08)70477-3 |
| [59] | Polk, C. and Postow, E. (1986) CRC Handbook of Biological Effects of Electromagnetic Fields. CRC Press, Boca Raton. |
| [60] | Barry, J.M. (2004) The Great Influenza: The Story of the Deadliest Pandemic in History. Penguin Books, London. |
| [61] | Carr, C.M. and Kim, P.S. (1993) Cell, 73, 823-832. https://doi.org/10.1016/0092-8674(93)90260-W |
| [62] | Sriwilaaijaroen, N. and Suzuki, Y. (2012) Proceedings of the Japan Academy, Ser. B, 88, 226-249. https://doi.org/10.2183/pjab.88.226 |
| [63] | Harrison, S. (2015) Viral Membrane Fusion. Part 2. https://www.youtube.com/watch?v=qcepGvFUM38 |
| [64] | Harrison, S. (2015) Virology, 479-480, 498-507. https://www.sciencedirect.com/science/article/pii/S004268221500183X https://doi.org/10.1016/j.virol.2015.03.043 |
| [65] | Saplakoglu, Y. (2020). https://www.livescience.com/coronavirus-spike-protein-structure.html |
| [66] | McAuley, J.L., et al. (2019) Frontiers in Microbiology, 10, 39-62. https://doi.org/10.3389/fmicb.2019.00039 |
| [67] | Kosik, I. and Yewdell, J.W. (2019) Viruses, 11, 346-364. https://doi.org/10.3390/v11040346 |
| [68] | Biswas, A., et al. (2020) Critical Reviews in Microbiology, 46, 182-193. |
| [69] | Gaymard, A., et al. (2016) Clinical Microbiology and Infection, 22, 975-983. https://doi.org/10.1016/j.cmi.2016.07.007 |
| [70] | Harrison, S. (2015) Non-Enveloped Virus Entry. https://www.youtube.com/watch?v=-1tSBwE1Wuk |
| [71] | Chang, C., et al. (2019) Proceedings of the National Academy of Sciences of the United States of America, 116, 18041-18049. https://doi.org/10.1073/pnas.1907733116 |
| [72] | Meessen, A. (2010) Ball Lightning: Bubbles of Electronic Plasma Oscillations. http://www.meessen.net/AMeessen/Ball-Lightning-Theory.pdf |
| [73] | Harvard Natural Science, Lecture Demonstrations: Shattering Wineglass. https://sciencedemonstrations.fas.harvard.edu/presentations/shattering-wineglass |
| [74] | Wrapp, D., et al. (2020) Science, 367, 1260-1263. https://science.sciencemag.org/content/367/6483/1260 https://doi.org/10.1126/science.abb2507 |
| [75] | Litak, G., et al. (2012) Nonlinear Oscillations of an Elastic Inverted Pendulum. 4th IEEE International Conference on Nonlinear Science and Complexity, Budapest, 6-11 August 2012, 113-116. http://litak.pollub.pl/20_nsc2012.pdf https://doi.org/10.1109/NSC.2012.6304737 |
| [76] | Kirson, E.D., et al. (2004) Disruption of Cancer Cell Replication by Alternative Electric Fields. Cancer Research, 64, 3288-3295. |
| [77] | Miller, J. (2007) Electric Fields Have Potential as Cancer Treatment. Physics Today, 60, 19. https://doi.org/10.1158/0008-5472.CAN-04-0083 https://physicstoday.scitation.org/doi/10.1063/1.2774085 |
| [78] | Heßling, M., et al. (2020) Ultraviolet Irradiation Doses for Coronavirus Inactivation. GMS Hygiene and Infection Control, 15, Doc08. https://www.egms.de/static/en/journals/dgkh/2020-15/dgkh000343.shtml |
| [79] | https://www.fda.gov/medical-devices/coronavirus-covid-19-and- medical-devices/uv-lights-and-lamps-ultraviolet-c-radiation-disinfection-and-coronavirus |
| [80] | Ventola, C.L. (2015) The Antibiotic Resistance Crisis Part 1 Causes and Threats. Part 2 Management Strategies and New Agents. Pharmacology & Therapeutics, 40, 277-283. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4378521 https://pubmed.ncbi.nlm.nih.gov/25987823/ |
| [81] | Lebedewa, T. und Driediger, E. (2001) Krebserreger Entdeckt. Driediger Verlag, Georgsmarienhütte. |
| [82] | Weber, A. (1969) über die Ursache der Krebskrankheit. Verlag Parcus, München. |
| [83] | Nordor, A.V. (2018) Open Biology, 8, Article ID: 180127. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6223206 https://doi.org/10.1098/rsob.180127 |
| [84] | Meessen, A. (2018) Journal of Modern Physics, 9, 2657-2724. https://www.scirp.org/pdf/JMP_2018122814430215.pdf https://doi.org/10.4236/jmp.2018.914165 |
| [85] | European Academies Science Advisory Council (2017) Homeopathic Products and Practices. https://easac.eu/fileadmin/PDF_s/reports_statements/EASAC_Homepathy_statement_web_final.pdf |
| [86] | Hartmann, L. and Lasco, C. (2020) Big-Pharma Labos Tout-Puissants. Arte, TV. Sept. 11, 2020. https://www.telez.fr/actus-tv/big-pharma-labos-tout-puissants-sur- arte-le-juteux-business-du-medicament/ |










